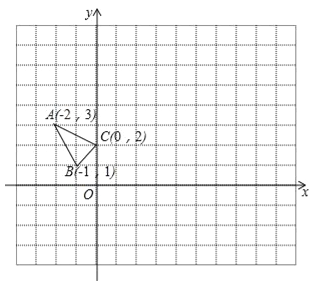
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.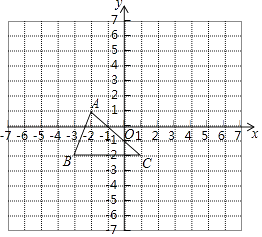
(1)在图中画出△A′B′C′;
(2)写出A′,B′的坐标;
(3)求三角形ABC的面积.
参考答案:
【答案】
(1)解:△A′B′C′如图所示.
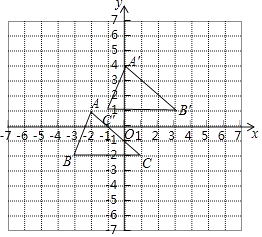
(2)解:A′(0,4),B′(3,1).
(3)解:S△ABC= ![]() 4×3=6.
4×3=6.
【解析】(1)依据三角形平移的方向和距离得到A′、B′、C′的位置;
(2)依据点A′、B′在坐标系中的位置可得到两点的坐标;
(3)先确定出三角形的底边长和高的长度,最后再根据三角形的面积公式计算即可.
【考点精析】关于本题考查的坐标与图形变化-平移,需要了解新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
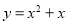 的图象,如图所示
的图象,如图所示(1)根据方程的根与函数图象之间的关系,将方程
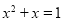 的根在图上近似地表示出来(描点),并观察图象,写出方程
的根在图上近似地表示出来(描点),并观察图象,写出方程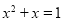 的根(精确到0.1).
的根(精确到0.1).(2)在同一直角坐标系中画出一次函数
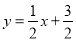 的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.
的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.(3)如图,点P是坐标平面上的一点,并在网格的格点上,请选择一种适当的平移方法,使平移后二次函数图象的顶点落在P点上,写出平移后二次函数图象的函数表达式,并判断点P是否在函数
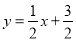 的图象上,请说明理由.
的图象上,请说明理由.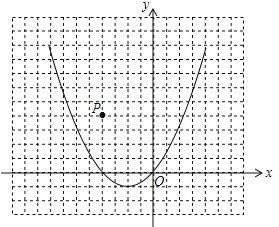
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次三项式x2﹣kx+9是一个完全平方式,则k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2﹣4x+1=0_____实数根(填“有”或“无”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.(不写解答过程,直接写出结果)
(1)若△A1B1C1与△ABC关于原点O成中心对称,则点A1的坐标为 ;
(2)将△ABC向右平移4个单位长度得到△A2B2C2,则点B2的坐标为 ;
(3)将△ABC绕O点顺时针方向旋转90°,则点C走过的路径长为 ;
(4)在x轴上找一点P,使PA+PB的值最小,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,直线
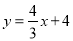 交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
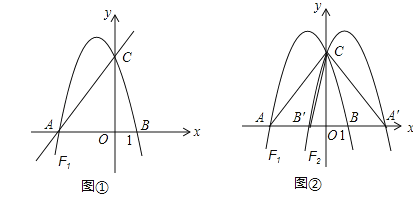
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
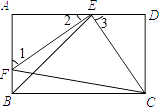
(1)求证:AE=DC;
(2)已知DC=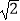 ,求BE的长.
,求BE的长.
相关试题

