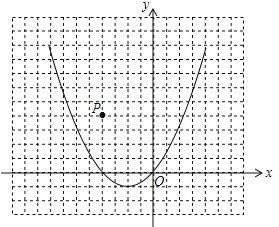
【题目】已知二次函数![]() 的图象,如图所示
的图象,如图所示
(1)根据方程的根与函数图象之间的关系,将方程![]() 的根在图上近似地表示出来(描点),并观察图象,写出方程
的根在图上近似地表示出来(描点),并观察图象,写出方程![]() 的根(精确到0.1).
的根(精确到0.1).
(2)在同一直角坐标系中画出一次函数![]() 的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.
的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值.
(3)如图,点P是坐标平面上的一点,并在网格的格点上,请选择一种适当的平移方法,使平移后二次函数图象的顶点落在P点上,写出平移后二次函数图象的函数表达式,并判断点P是否在函数![]() 的图象上,请说明理由.
的图象上,请说明理由.
参考答案:
【答案】(1)![]() ≈﹣1.6,
≈﹣1.6,![]() ≈0.6;(2)当x<﹣1.5或x>1时;(3)
≈0.6;(2)当x<﹣1.5或x>1时;(3)![]() ,在.
,在.
【解析】
试题分析:(1)令y=0求得抛物线与x的交点坐标,从而可确定出1个单位长度等于小正方形边长的4倍,接下来作直线y=1,找出直线y=1与抛物线的交点,直线与抛物线的交点的横坐标即可方程的解;
(2)先求得直线上任意两点的坐标,然后画出过这两点的直线即可得到直线![]() 的函数图象,然后找出一次函数图象位于直线下方部分x的取值范围即可;
的函数图象,然后找出一次函数图象位于直线下方部分x的取值范围即可;
(3)先依据抛物线的顶点坐标和点P的坐标,确定出抛物线移动的方向和距离,然后依据抛物线的顶点式写出抛物线的解析式即可,将点P的坐标代入函数解析式,如果点P的坐标符合函数解析式,则点P在直线上,否则点P不在直线上.
试题解析:(1)∵令y=0得:![]() ,解得:
,解得:![]() ,
,![]() ,∴抛物线与x轴的交点坐标为(0,0),(﹣1,0).
,∴抛物线与x轴的交点坐标为(0,0),(﹣1,0).
作直线y=1,交抛物线与A、B两点,分别过A、B两点,作AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,点C和点D的横坐标即为方程的根.
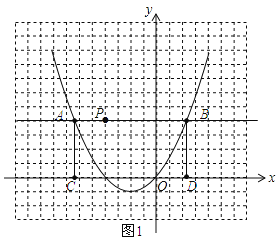
根据图形可知方程的解为![]() ≈﹣1.6,
≈﹣1.6,![]() ≈0.6.
≈0.6.
(2)∵将x=0代入![]() 得y=
得y=![]() ,将x=1代入得:y=2,∴直线
,将x=1代入得:y=2,∴直线![]() 经过点(0,
经过点(0,![]() ),(1,2).直线
),(1,2).直线![]() 的图象如图所示:
的图象如图所示:
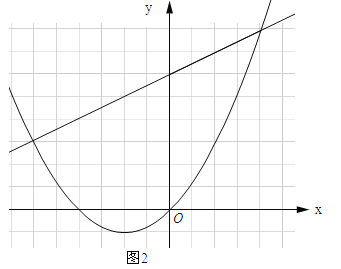
由函数图象可知:当x<﹣1.5或x>1时,一次函数的值小于二次函数的值.
(3)先向上平移![]() 个单位,再向左平移
个单位,再向左平移![]() 个单位,平移后的顶点坐标为P(﹣1,1).
个单位,平移后的顶点坐标为P(﹣1,1).
平移后的表达式为y=(x+1)2+1,即![]() .
.
点P在![]() 的函数图象上.
的函数图象上.
理由:∵把x=﹣1代入得y=1,∴点P的坐标符合直线的解析式,∴点P在直线![]() 的函数图象上.
的函数图象上.
-
科目: 来源: 题型:
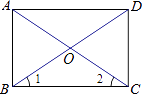
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.求证:四边形ABCD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:菱形ABCD的两条对角线AC,BD交于点O,BE∥AC,CE∥BD.
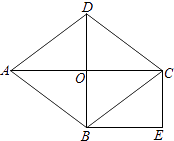
(1)若AC=8,BD=6,求AB的长;
(2)求证:四边形OBEC为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次三项式x2﹣kx+9是一个完全平方式,则k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2﹣4x+1=0_____实数根(填“有”或“无”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
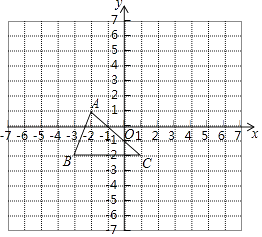
(1)在图中画出△A′B′C′;
(2)写出A′,B′的坐标;
(3)求三角形ABC的面积.
相关试题

