搜索
【题目】如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．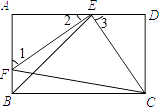 
（1）求证：AE=DC；
（2）已知DC= 
，求BE的长．
参考答案：
【答案】
（1）证明：在矩形ABCD中，∠A=∠D=90°，
∴∠1+∠2=90°，
∵EF⊥EC，
∴∠FEC=90°，
∴∠2+∠3=90°，
∴∠1=∠3，
在△AEF和△DCE中，
，
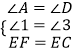∴△AEF≌△DCE（AAS），
∴AE=DC
（2）解：由（1）得AE=DC，
∴AE=DC= 
，
在矩形ABCD中，AB=CD= ，
在R△ABE中，AB2+AE2=BE2，即（ ）2+（ ）2=BE2，
∴BE=2
【解析】（1）根据矩形的性质和已知条件可证明△AEF≌△DCE，可证得AE=DC；（2）由（1）可知AE=DC，在Rt△ABE中由勾股定理可求得BE的长．
【考点精析】根据题目的已知条件，利用勾股定理的概念和矩形的性质的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；矩形的四个角都是直角，矩形的对角线相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．
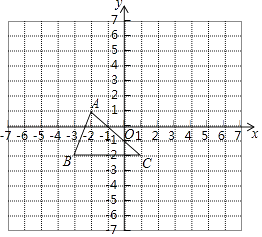
（1）在图中画出△A′B′C′；
（2）写出A′，B′的坐标；
（3）求三角形ABC的面积． -
科目： 来源： 题型：
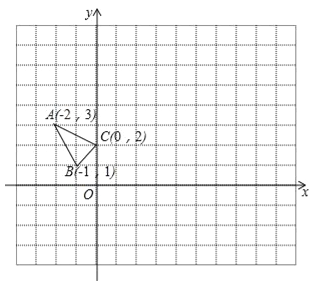
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示．（不写解答过程，直接写出结果）
（1）若△A1B1C1与△ABC关于原点O成中心对称，则点A1的坐标为 ；
（2）将△ABC向右平移4个单位长度得到△A2B2C2，则点B2的坐标为 ；
（3）将△ABC绕O点顺时针方向旋转90°，则点C走过的路径长为 ；
（4）在x轴上找一点P，使PA+PB的值最小，则点P的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，直线
交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．（1）求抛物线F1所表示的二次函数的表达式；
（2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC﹣S△BOC，求S最大时点M的坐标及S的最大值；
（3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．
-
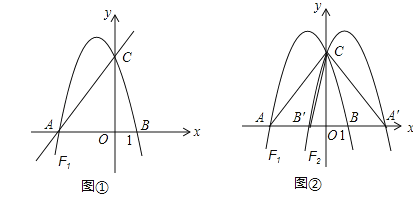
科目： 来源： 题型：
查看答案和解析>>【题目】为了抓住保国寺建寺1000年的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．
（1）求购进A、B两种纪念品每件各需多少元？
（2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
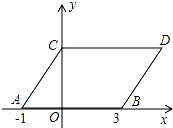
（1）求点C，D的坐标；
（2）若在y轴上存在点 M，连接MA，MB，使S△MAB=S平行四边形ABDC ， 求出点M的坐标．
（3）若点P在直线BD上运动，连接PC，PO．
①若P在线段BD之间时（不与B，D重合），求S△CDP+S△BOP的取值范围；
②若P在直线BD上运动，请直接写出∠CPO、∠DCP、∠BOP的数量关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF，ED交线段AB于点G，ED的延长线交线段OA于点H，连CH、CG．
（1）求证：△CBG≌△CDG；
（2）求∠HCG的度数；并判断线段HG、OH、BG之间的数量关系，说明理由；
（3）连结BD、DA、AE、EB得到四边形AEBD，在旋转过程中，当G点在何位置时四边形AEBD是矩形？请说明理由并求出点H的坐标．
相关试题
