【题目】将![]() 的边
的边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,边
,边![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,![]() ,连接
,连接![]() ,作
,作![]() 的中线
的中线![]() .
.
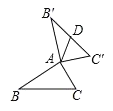
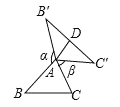

图① 图② 图③
(初步感知)
(1)如图①,当![]() ,
,![]() 时,
时,![]() 的长为 ;
的长为 ;
(探究运用)
(2)如图②,![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
(应用延伸)
(3)如图③,已知等腰![]() ,
,![]() ,延长
,延长![]() 到
到![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一周得到
顺时针旋转一周得到![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的长度(用含
的长度(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
参考答案:
【答案】(1)2;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() .
.
【解析】
(1)只要证明BC=B′C′=4,再利用直角三角形斜边中线的性质即可解决问题;
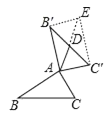
(2)如图①中,延长AD到E,使得DE=AD.连接EB′,EC′.只要证明△AB′E≌△BAC,即可解决问题;
(3)分两种情形,利用(2)中结论以及勾股定理计算即可;
(1)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直角三角形
是直角三角形![]() 斜边的中线,
斜边的中线,
![]() .
.
故答案为![]() .
.
(2)证明:如图中,延长![]() 到
到![]() ,使得
,使得![]() .连接
.连接![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)①如图中,作![]() 的中线
的中线![]() .
.
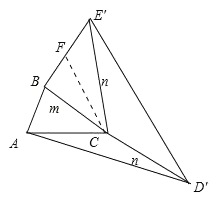
在![]() 中,
中,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
由(2)可知:![]() .
.
②如图中,作![]() 的中线
的中线![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() .
.
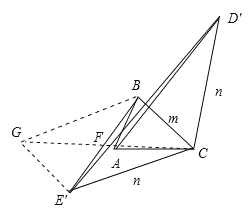
同法可证:![]() ,
,
![]() ,
,
由①可知,![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是______事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每6个人中会有1人抽中一等奖、2人抽中二等奖,若袋中共有18个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中增加3个黄球,那么抽中一等奖的概率会怎样变化?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E、F在BD上,且AB=BE=DF.
(1)求证:四边形AECF是菱形;
(2)若正方形的边长为2,求四边形AECF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,CE与BF相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)□ABCD应满足什么条件时,四边形EHFG是矩形?并说明理由;
(3)□ABCD应满足什么条件时,四边形EHFG是正方形?(不要说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图(图1,图2).请你根据图中提供的信息,解答以下问题:

(1)该班共有 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为 ;
(4)若全校有2000名学生,则“其他”部分的学生人数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:
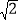 ≈1.4,
≈1.4,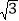 ≈1.7)
≈1.7)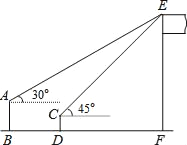
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;
(2)平移△ABC:若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(3)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
相关试题

