【题目】有理数计算题:(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)-6ab+ba+8ab
(6)-5a+2(3a-2)-(3a-7)
参考答案:
【答案】(1)12;(2)15;(3)-18;(4)9;(5)3ab;(6)-2a+3.
【解析】
(1)根据有理数的加法法则与加法交换结合律,即可求解;
(2)根据有理数的混合运算以及分配律,即可求解;
(3)根据有理数的混合运算,即可求解;
(4)根据含乘方的有理数的混合运算,即可求解;
(5)根据合并同类项法则,即可求解;
(6)根据整式的加减法法则,即可求解.
(1)原式=![]()
=![]()
=12;
(2)原式=![]()
=![]()
=15;
(3)原式=![]()
=![]()
=-18;
(4)原式=![]()
=![]()
=9;
(5)原式=-6ab+ba+8ab
=3ab;
(6)原式=-5a+6a-4-3a+7
=-2a+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
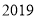 年春节期间,某物业公司组织两个小区的部分居民去旅游,已知某景点的门票价格如下表:
年春节期间,某物业公司组织两个小区的部分居民去旅游,已知某景点的门票价格如下表:购票人数
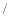 人
人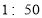
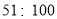
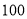 以上
以上每人门票价
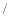 元
元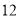
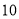
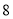
小区①的人数少于
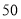 人,小区②的人数多于
人,小区②的人数多于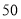 人且少于
人且少于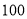 人,如果两小区单独购票,则一共支付
人,如果两小区单独购票,则一共支付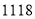 元;如果两小区联合起来作为一个团体购票,因为人数超过
元;如果两小区联合起来作为一个团体购票,因为人数超过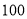 人,只需花费
人,只需花费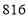 元请问:
元请问:(1)两个小区各有多少人?
(2)团体购票与单独购票相比较,两个小区各节省了多少钱?
(3)若小区①单独购票,请为小区①设计一种最省钱的购买方案,并计算能省多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:71=7,72=49,73=343,74=2 401,75=16 807,76=117 649,…,那么:71+72+73+…+72 016的末位数字是( )
A. 9B. 7C. 6D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】按如下规律摆放三角形:
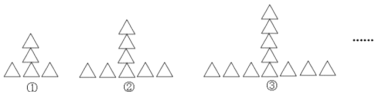
(1)图④中分别有多少个三角形?
(2)按上述规律排列下去,第n个图形中有多少个三角形?
(3)按上述规律排列下去,第2014个图形中有多少个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。

(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
-
科目: 来源: 题型:
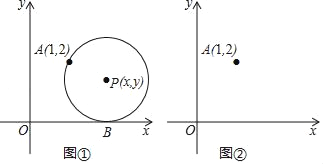
查看答案和解析>>【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
相关试题

