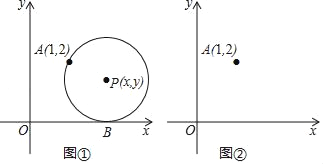
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
参考答案:
【答案】(1)![]() ;(2)图象为开口向上的抛物线,见解析;(3)点A;x轴;(4)
;(2)图象为开口向上的抛物线,见解析;(3)点A;x轴;(4)![]()
【解析】(1)由题意得到AP=PB,求出y的值,即为圆P的半径;
(2)利用两点间的距离公式,根据AP=PB,确定出y关于x的函数解析式,画出函数图象即可;
(3)类比圆的定义描述此函数定义即可;
(4)画出相应图形,求出m的值,进而确定出所求角的余弦值即可.
(1)由x=2,得到P(2,y),
连接AP,PB,
∵圆P与x轴相切,
∴PB⊥x轴,即PB=y,
由AP=PB,得到![]() =y,
=y,
解得:y=![]() ,
,
则圆P的半径为![]() ;
;
(2)同(1),由AP=PB,得到(x﹣1)2+(y﹣2)2=y2,
整理得:y=![]() (x﹣1)2+1,即图象为开口向上的抛物线,
(x﹣1)2+1,即图象为开口向上的抛物线,
画出函数图象,如图②所示;
(3)给(2)中所得函数图象进行定义:此函数图象可以看成是到点A的距离等于到x轴的距离的所有点的集合;
故答案为:点A;x轴;
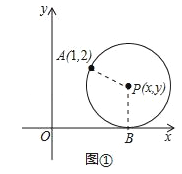
(4)连接CD,连接AP并延长,交x轴于点F,交CD于E,
设PE=a,则有EF=a+1,ED=![]() ,
,
∴D坐标为(1+![]() ,a+1),
,a+1),
代入抛物线解析式得:a+1=![]() (1﹣a2)+1,
(1﹣a2)+1,
解得:a=﹣2+![]() 或a=﹣2﹣
或a=﹣2﹣![]() (舍去),即PE=﹣2+
(舍去),即PE=﹣2+![]() ,
,
在Rt△PED中,PE=![]() ﹣2,PD=1,
﹣2,PD=1,
则cos∠APD=![]() =
=![]() ﹣2.
﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数计算题:(1)
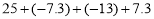
(2)
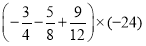
(3)
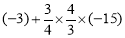
(4)
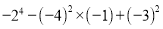
(5)-6ab+ba+8ab
(6)-5a+2(3a-2)-(3a-7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】按如下规律摆放三角形:
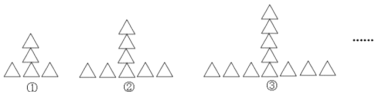
(1)图④中分别有多少个三角形?
(2)按上述规律排列下去,第n个图形中有多少个三角形?
(3)按上述规律排列下去,第2014个图形中有多少个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。

(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为( )
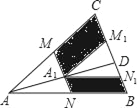
A. 14 B. 21 C. 28 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:
 微信、
微信、 支付宝、
支付宝、 现金、
现金、 其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.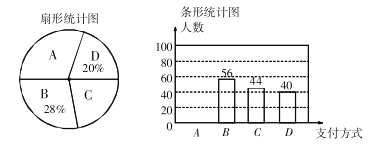
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中
 种支付方式所对应的圆心角为___________度;
种支付方式所对应的圆心角为___________度;(3)若该超市这一周内有3200名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
-
科目: 来源: 题型:
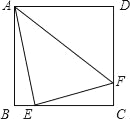
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于_____.
相关试题

