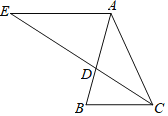
【题目】如图,在△ABC中,AB=AC,∠BAC=36°,CD是∠ACB的平分线交AB于点D,过点A作AE∥BC,交CD的延长线于点E.
(1)求∠ADC的度数;
(2)求证:AE=AC
(3)试问△ADE是等腰三角形吗?请说明理由.
参考答案:
【答案】(1)∠ADC=108°;(2)见解析;(3)△ADE是等腰三角形,理由见解析
【解析】
(1)关键等腰三角形性质和三角形内角和定理求出∠B=∠ACB=72°,求出∠DCB,根据三角形外角性质求出即可;
(2)先判断出∠BCE=∠ACE,再判断出∠BCE=∠E,即可得出结论;
(3)根据平行线求出∠EAD,根据三角形内角和定理求出∠ADE,即可得出答案
解:(1)∵AB=AC,∠BAC=36°,
∴∠B=∠ACB=![]() (180°-∠BAC)=72°,
(180°-∠BAC)=72°,
∵CD是∠ACB的平分线,
∴∠DCB=![]() ∠ACB=36°;
∠ACB=36°;
∴∠ADC=∠B+∠DCB=72°+36°=108°,
(2)AE=AC,证明如下:
∵CD是∠ACB的平分线,
∴∠BCE=∠ACE,
∵AE∥BC,
∴∠BCE=∠E,
∴∠ACE=∠E,
∴AE=AC;
(3)△ADE是等腰三角形,
理由是:∵AE∥BC,
∴∠EAB=∠B=72°,
∵∠B=72°,∠DCB=36°,
∴∠ADE=∠BDC=180°-72°-36°=72°,
∴∠EAD=∠ADE,
∴AE=DE,
即△ADE是等腰三角形.
-
科目: 来源: 题型:
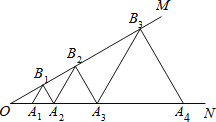
查看答案和解析>>【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△An+1Bn+1An+2的边长为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按
 ,
, ,
, ,
, 四个等级进行统计,制成了如下不完整的统计图.(说明:
四个等级进行统计,制成了如下不完整的统计图.(说明: 级:8分—10分,
级:8分—10分, 级:7分—7.9分,
级:7分—7.9分, 级:6分—6.9分,
级:6分—6.9分, 级:1分—5.9分)
级:1分—5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,
 对应的扇形的圆心角是_______度;
对应的扇形的圆心角是_______度;(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在_______等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到
 级的学生有多少人?
级的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在平面直角坐标系中点A(a,b)点B(a,0),且满足|2a-b|+(b-4)2=0.
(1)求点A、点B的坐标;
(2)已知点C(0,b),点P从B点出发沿x轴负方向以1个单位每秒的速度移动.同时点Q从C点出发,沿y轴负方向以2个单位每秒的速度移动,某一时刻,如图所示且S阴=
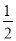 S四边形OCAB,求点P移动的时间;
S四边形OCAB,求点P移动的时间;(3)在(2)的条件下,AQ交x轴于M,作∠ACO,∠AMB的角平分线交于点N,判断
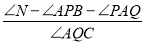 是否
是否 为定值,若是定值求其值;若不是定值,说明理由.
为定值,若是定值求其值;若不是定值,说明理由.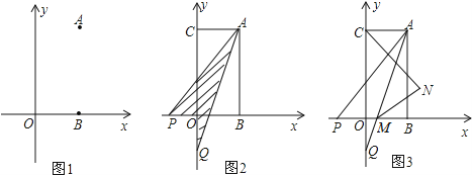
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列计算过程,猜想立方根.
 =1
=1 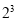 =8
=8  =27
=27 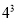 =64
=64  =125
=125 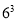 =216
=216 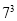 =343
=343 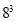 =512
=512 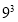 =729
=729 (1)小明是这样试求出19683的立方根的,先估计19683的立方根的个位数, 猜想它的个位数为 , 又由
 <19000<
<19000< 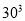 ,猜想19683的立方根十位数为 ,验证得19683的立方根是 .
,猜想19683的立方根十位数为 ,验证得19683的立方根是 .(2)请你根据(1)中小明的方法,完成如下填空:
①
 = ; ②
= ; ②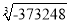 = ;③
= ;③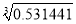 = .
= . -
科目: 来源: 题型:
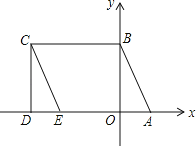
查看答案和解析>>【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=
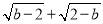 ﹣3.
﹣3.(1)直接写出点C的坐标 ;
(2)直接写出点E的坐标 ;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
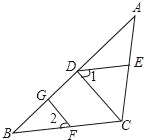
查看答案和解析>>【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
相关试题

