搜索
【题目】某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长37米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的面积最大？如图是两位学生争议的情境：请根据上面的信息，解决问题： 
（1）设AB=x米（x＞0），试用含x的代数式表示BC的长；
（2）请你判断谁的说法正确，为什么？
参考答案：
【答案】
（1）解：设AB=x米，可得：BC=37+3﹣2x=40﹣2x
（2）解：小英说法正确；
矩形面积S=x（40﹣2x）=﹣2（x﹣10）2+200，
∴当x=10时，S取最大值，
此时x≠40﹣2x，∴面积最大的不是正方形
【解析】（1）设AB=x米，根据等式x+x+BC=37+3，可以求出BC的表达式；（2）得出面积关系式，根据所求关系式进行判断即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
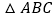中，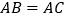
，D，E，F分别为AB，BC，CA上的点，且
，
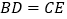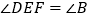．（1）求证：
≌
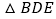；（2）若
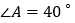，求
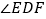的度数．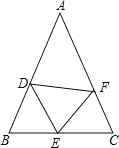
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点M为直线AB上一动点，
都是等边三角形，连接BN 
求证： 
；
分别写出点M在如图2和图3所示位置时，线段AB、BM、BN三者之间的数量关系
不需证明
；
如图4，当
时，证明： 
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，⊙O的内接△ABC中，∠BAC=45°，∠ABC=15°，AD∥OC并交BC的延长线于D点，OC交AB于E点．
（1）求∠D的度数；
（2）求证：AC2=ADCE． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形网格中的每个小正方形边长都是1．请同学们利用网格线进行画图：
(1)在图1中，画一个顶点为格点、面积为5的正方形；
(2)在图2中，已知线段AB、CD，画线段EF，使它与AB、CD组成轴对称图形；(要求画出所有符合题意的线段)
(3)在图3中，找一格点D，满足：①到CB、CA的距离相等；②到点A、C的距离相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点F，G分别在△ADE的AD，DE边上，C，B依次为GF延长线上两点，AB=AD，∠BAF=∠CAE，∠B=∠D．
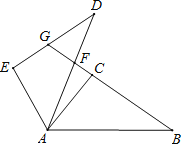
（1）求证：BC=DE；
（2）若∠B=35°，∠AFB=78°，直接写出∠DGB的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：
如示意图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD=1.2m，CE=0.8m，CA=30m（点A，E，C在同一直线上）．已知小明的身高EF是1.7m，请你帮小明求出楼高AB．（结果精确到0.1m）
相关试题
