Question

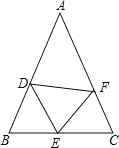
【题目】如图，中，，D，E，F分别为AB，BC，CA上的点，且，．

（1）求证：≌；

（2）若，求的度数．

Answer 1

【答案】（1）证明见解析；（2）55°．

【解析】

（1）根据三角形外角的性质可得到∠CEF=∠BDE，可证△BDE≌△CEF；

（2）由（1）可得DE=FE，即△DEF是等腰三角形，由等腰三角形的性质可求出∠B=70°，即∠DEF=∠B=70°，从而求出∠EDF的度数．

（1）∵∠DEC=∠B+∠BDE=∠CEF+∠DEF，∠DEF=∠B，∴∠CEF=∠BDE．

∵AB=AC，∴∠C=∠B．

又∵CE=BD，∴△BDE≌△CEF．

（2）∵△BDE≌△CEF，∴DE=FE．

∴△DEF是等腰三角形，∴∠EDF=∠EFD．

∵AB=AC，∠A=40°，∴∠B=70°．

∵∠DEF=∠B，∴∠DEF=70°，∴∠EDF=∠EFD=×（180°﹣70°）=55°．