【题目】如图,点F,G分别在△ADE的AD,DE边上,C,B依次为GF延长线上两点,AB=AD,∠BAF=∠CAE,∠B=∠D.
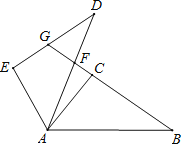
(1)求证:BC=DE;
(2)若∠B=35°,∠AFB=78°,直接写出∠DGB的度数.
参考答案:
【答案】(1)见解析;(2)67°.
【解析】
试题分析:(1)由∠BAF=∠CAE,等式两边同时减去∠CAF,可得出∠BAC=∠DAE,再由AB=AD,∠B=∠D,理由ASA得出△ABC≌△ADE,利用全等三角形的对应边相等可得证;
(2)由∠B=∠D,以及一对对顶角相等,利用两对对应角相等的两三角形相似得到三角形ABF与三角形DGF相似,由相似三角形的对应角相等得到∠DGB=∠BAD,在三角形AFB中,由∠B及∠AFB的度数,利用三角形的内角和定理求出∠BAD的度数,进而得到∠DGB的度数.
(1)证明:∵∠BAF=∠CAE,
∴∠BAF﹣∠CAF=∠CAE﹣∠CAF,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
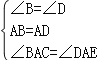 ,
,
∴△ABC≌△ADE(ASA),
∴BC=DE;
(2)解:∠DGB的度数为67°,理由为:
∵∠B=∠D,∠AFB=∠GFD,
∴△ABF∽△GDF,
∴∠DGB=∠BAD,
在△AFB中,∠B=35°,∠AFB=78°,
∴∠DGB=∠BAD=180°﹣35°﹣78°=67°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正六边形的每个外角都是30°,那么这个多边形的内角和为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
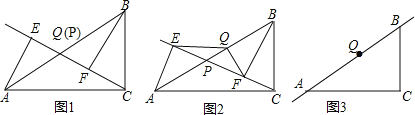
-
科目: 来源: 题型:
查看答案和解析>>【题目】用18cm长的细绳围成一个边长为4cm 的等腰三角形,则这个等腰三角形腰长为_______cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=4,AC=3,BC=5,动点P从点C出发,沿着CB方向运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
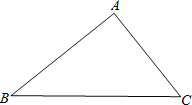
(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是( )
A.0是正数也是有理数
B.两数之积为正,这两数同为正
C.几个数相乘,积的符号由负因数的个数决定
D.互为相反数的两个数的绝对值相等.
相关试题

