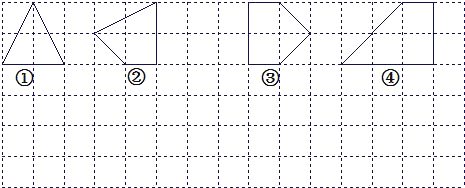
【题目】(本题满分11分)让我们一起探索有趣的“皮克定理”:用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
 .
.
(1)上图中的格点多边形,其内部都只有一个格点,请完成下表,并写出S与x之间的关系式:S=______.

(2)探索:在上面网格图中画出四个格点多边形,其内部都只有两个格点,并写出所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式:S=______;
(3)猜想:当格点多边形内部有且只有n个格点时,S与x之间的关系式是:S=______.
参考答案:
【答案】(1)![]() ,3 ,
,3 , ![]() ;(2)作图见解析,
;(2)作图见解析, ![]() +1;(3)
+1;(3)![]() +(n-1).
+(n-1).
【解析】试题分析:(1)分别算出②和③的面积,再探索规律;(2)先画出四个图形,再求出四个图形的面积,最后探索面积S和x的关系;(3)由(1)(2)问求出的S与x的关系探索规律.
解:(1)图②的面积为S=4-![]() ×1×2-
×1×2-![]() ×1×1=
×1×1=![]() ,图③的面积为S=4-
,图③的面积为S=4-![]() ×1×1-
×1×1-![]() ×1×1=3,
×1×1=3,
根据2, ![]() ,3,4对应4,5,6,8,可知S和x的关系为S=
,3,4对应4,5,6,8,可知S和x的关系为S=![]() x;
x;
故答案为![]() ,3,
,3, ![]() .
.
(2)如图,分别画出四个格点多边形⑤⑥⑦⑧,其内部都只有两个格点.
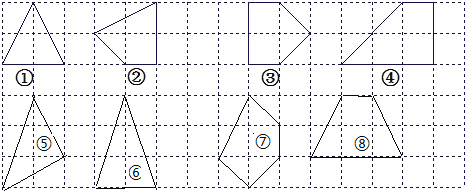
图⑤中x=3,S=![]() ;图⑥中,x=4,S=3;图⑦中,x=5,S=
;图⑥中,x=4,S=3;图⑦中,x=5,S=![]() ;图⑧中,x=6,S=4.
;图⑧中,x=6,S=4.
则可知此时S= ![]() +1;
+1;
(3)当n=1时,S= ![]() ;
;
当n=2时,S= ![]() +1.
+1.
则可知![]() +(n-1).
+(n-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BC,AB⊥BC,AB=3. 点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N. 当点B′为线段MN的三等分点时,BE的长为__________________.

-
科目: 来源: 题型:
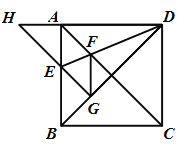
查看答案和解析>>【题目】如图
 ,正方形
,正方形 的边长为
的边长为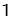 ,
,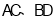 是对角线,将
是对角线,将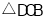 绕点
绕点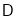 顺时针旋转450得到
顺时针旋转450得到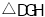 ,
, 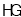 交
交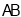 于点
于点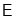 ,连接
,连接 交
交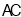 于点
于点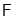 ,连接
,连接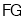 ,则下列结论:
,则下列结论: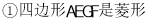
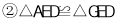

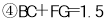
其中正确的结论是 .(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=
 ,求正方形ABCD的边长;
,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线被第三条直线所截,那么下面 说法正确的上是( )
A.同位角相等
B.内错角相等
C.同旁内角互补
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度
 (cm)与所挂物体的质量
(cm)与所挂物体的质量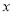 (kg)之间的关系如下表:
(kg)之间的关系如下表:所挂物体的质量
 (kg)
(kg)0
1
2
3
4
5
6
弹簧的长度
 (cm)
(cm)15
15.6
16.2
16.8
17.4
18
18.6
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出
 与
与 之间的关系式;
之间的关系式;(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣2是方程x2+mx﹣6=0的一个根,则方程的另一个根是 .
相关试题

