【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.

参考答案:
【答案】(1)1;(2)CN=![]() CM,理由详见解析.
CM,理由详见解析.
【解析】
试题分析:(1)根据正方形的性质可得△ABD是等腰直角三角形,再由勾股定理可得2AB2=BD2,即可求得AB=1;(2)根据等腰三角形的性质可得CE⊥AF,再证得∠BAF=∠BCN,利用AAS证得△ABF≌△CBN,根据全等三角形的性质可得AF=CN,再证△ABF∽△COM,根据相似三角形的性质和正方形的性质即可证得CN=![]() CM.
CM.
试题解析:(1)∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD=![]() ,
,
∴AB=1,
∴正方形ABCD的边长为1;
(2)CN=![]() CM.
CM.
证明:∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,
∴∠AEN=∠CBN=90°,
∵∠ANE=∠CNB,
∴∠BAF=∠BCN,
在△ABF和△CBN中,
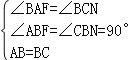 ,
,
∴△ABF≌△CBN(AAS),
∴AF=CN,
∵∠BAF=∠BCN,∠ACN=∠BCN,
∴∠BAF=∠OCM,
∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠ABF=∠COM=90°,
∴△ABF∽△COM,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
即CN=![]() CM.
CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )

A.
 B.2
B.2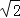 C.
C.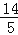 D.10﹣5
D.10﹣5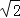
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BC,AB⊥BC,AB=3. 点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N. 当点B′为线段MN的三等分点时,BE的长为__________________.

-
科目: 来源: 题型:
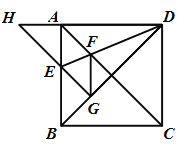
查看答案和解析>>【题目】如图
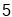 ,正方形
,正方形 的边长为
的边长为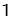 ,
,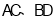 是对角线,将
是对角线,将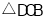 绕点
绕点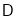 顺时针旋转450得到
顺时针旋转450得到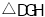 ,
, 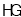 交
交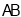 于点
于点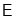 ,连接
,连接 交
交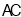 于点
于点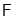 ,连接
,连接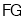 ,则下列结论:
,则下列结论: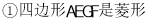
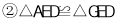

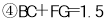
其中正确的结论是 .(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分11分)让我们一起探索有趣的“皮克定理”:用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
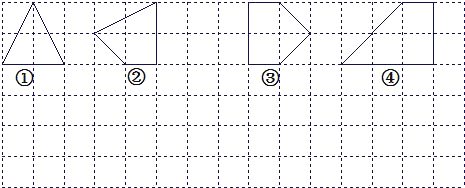 .
.(1)上图中的格点多边形,其内部都只有一个格点,请完成下表,并写出S与x之间的关系式:S=______.

(2)探索:在上面网格图中画出四个格点多边形,其内部都只有两个格点,并写出所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式:S=______;
(3)猜想:当格点多边形内部有且只有n个格点时,S与x之间的关系式是:S=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线被第三条直线所截,那么下面 说法正确的上是( )
A.同位角相等
B.内错角相等
C.同旁内角互补
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度
 (cm)与所挂物体的质量
(cm)与所挂物体的质量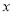 (kg)之间的关系如下表:
(kg)之间的关系如下表:所挂物体的质量
 (kg)
(kg)0
1
2
3
4
5
6
弹簧的长度
 (cm)
(cm)15
15.6
16.2
16.8
17.4
18
18.6
(1)上表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出
 与
与 之间的关系式;
之间的关系式;(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度。
相关试题

