【题目】如图,已知AD∥BC,AB⊥BC,AB=3. 点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N. 当点B′为线段MN的三等分点时,BE的长为__________________.

参考答案:
【答案】![]() 或
或![]() .
.
【解析】
试题分析:根据题意可得四边形ABNM是矩形,所以AB=MN=3,AM=BN,根据折叠的性质可得AB=AB’,BE=B’E,点B′为线段MN的三等分点时,分两种情况:①当MB’=1,B’N=2时,在Rt△AMB’中,由勾股定理求得AM=![]() ,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得
,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得![]() ,解得x=
,解得x=![]() ;②当MB’=2,B’N=1时,在Rt△AMB’中,由勾股定理求得AM=
;②当MB’=2,B’N=1时,在Rt△AMB’中,由勾股定理求得AM=![]() ,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得
,设BE==B’E=x,在Rt△ENB’中,由勾股定理可得![]() ,解得x=
,解得x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是线段AC的中点,N是线段BC的中点.

(1)如果AC=8cm,BC=6cm,求MN的长.
(2)如果AM=5cm,CN=2cm,求线段AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )

A.
 B.2
B.2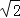 C.
C.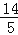 D.10﹣5
D.10﹣5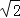
-
科目: 来源: 题型:
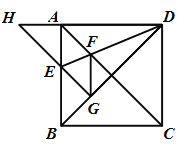
查看答案和解析>>【题目】如图
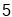 ,正方形
,正方形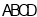 的边长为
的边长为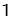 ,
,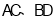 是对角线,将
是对角线,将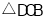 绕点
绕点 顺时针旋转450得到
顺时针旋转450得到 ,
,  交
交 于点
于点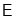 ,连接
,连接 交
交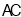 于点
于点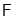 ,连接
,连接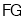 ,则下列结论:
,则下列结论: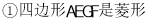
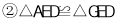

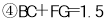
其中正确的结论是 .(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=
 ,求正方形ABCD的边长;
,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分11分)让我们一起探索有趣的“皮克定理”:用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x.
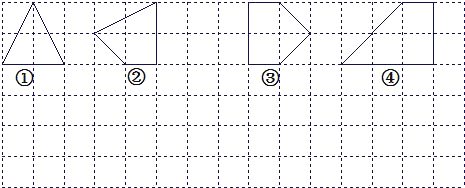 .
.(1)上图中的格点多边形,其内部都只有一个格点,请完成下表,并写出S与x之间的关系式:S=______.

(2)探索:在上面网格图中画出四个格点多边形,其内部都只有两个格点,并写出所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式:S=______;
(3)猜想:当格点多边形内部有且只有n个格点时,S与x之间的关系式是:S=______.
相关试题

