【题目】如图,正方形OABC的顶点O在坐标原点,顶点A的坐标为(4,3) 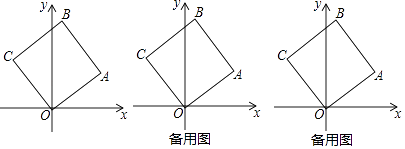
(1)顶点C的坐标为( , ),顶点B的坐标为( , );
(2)现有动点P、Q分别从C、A同时出发,点P沿线段CB向终点B运动,速度为每秒1个单位,点Q沿折线A→O→C向终点C运动,速度为每秒k个单位,当运动时间为2秒时,以P、Q、C为顶点的三角形是等腰三角形,求此时k的值.
(3)若正方形OABC以每秒 ![]() 个单位的速度沿射线AO下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
个单位的速度沿射线AO下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
参考答案:
【答案】
(1)﹣3;4;1;7
(2)
解:由题意得,AO=CO=BC=AB=5,
当t=2时,CP=2.
①当点Q在OA上时,∵PQ≥AB>PC,
∴只存在一点Q,使QC=QP.
作QD⊥PC于点D(如图2中),则CD=PD=1,
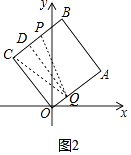
∴QA=2k=5﹣1=4,
∴k=2.②当点Q在OC上时,由于∠C=90°所以只存在一点Q,使CP=CQ=2,
∴2k=10﹣2=8,∴k=4.
综上所述,k的值为2或4
(3)
解:①当点A运动到点O时,t=3.
当0<t≤3时,设O’C’交x轴于点E,作A’F⊥x轴于点F(如图3中).
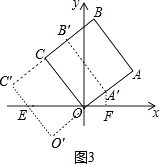
则△A’OF∽△EOO’,
∴ ![]() =
= ![]() =
= ![]() ,OO′=
,OO′= ![]() t,
t,
∴EO′= ![]() t,
t,
∴S= ![]() t2.②当点C运动到x轴上时,t=4
t2.②当点C运动到x轴上时,t=4
当3<t≤4时(如图4中),设A’B’交x轴于点F,
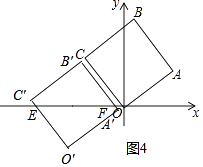
则A’O=A′O= ![]() t﹣5,
t﹣5,
∴A′F= ![]() .
.
∴S= ![]() (
( ![]() +
+ ![]() t)×5=
t)×5= ![]() .
.
综上所述,S= 
【解析】解:(1)如图1中,作CM⊥x轴于,AN⊥x轴于N.连接AC、BO交于点K.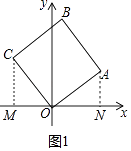
易证△AON≌△COM,可得CM=ON=4,OM=AN=3,
∴C(﹣3,4),∵CK=AK,OK=BK,
∴K( ![]() ,
, ![]() ),B(1,7),
),B(1,7),
所以答案是﹣3,4,1,7
【考点精析】本题主要考查了正方形的性质和坐标与图形变化-平移的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:
计算代数式
 (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的 (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.x
……
0.25
0.5
1
10
100
1000
10000
……

……
……
下面是小东计算代数式
 (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:x
……
0.25
0.5
1
10
100
1000
10000
……

……
2
1

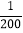
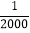
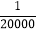
……
(1)上表是
 (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式 的值;
的值;(2)随着x值的增大,代数式
 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);(3)当x值无限增大时,代数式
 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=2x-4
(1)画出函数的图象;
(2)判断点A(1,-2),B(2,1)是否在该函数的图象上.
(3)已知点A(-2,b)在该函数图像上,求b值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“探究性学习”课中,李老师设计了如下数表:
n
2
3
4
5
…
a
22﹣1
32﹣1
42﹣1
52﹣1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)用含自然数n(n>1)的代数式表示:a,b,c.
(2)当c=101时,求n的值;
(3)用等式表示a、b、c之间的数量关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数的图像与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)一次函数的函数关系式;
(2)若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴上从左到右的三个点A,B,C所对应数的分别为a,b,c.其中点A、点B两点间的距离AB的长是2019,点B、点C两点间的距离BC的长是1000,

(1)若以点C为原点,直接写出点A,B所对应的数;
(2)若原点O在A,B两点之间,求|a|+|b|+|b﹣c|的值;
(3)若O是原点,且OB=19,求a+b﹣c的值.
相关试题

