【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
参考答案:
【答案】(1)(0,3);(2)![]() .
.
【解析】
试题(1)在Rt△AOB中,由勾股定理得到OB=3,即可得出点B的坐标;
(2)由![]() =
=![]() BCOA,得到BC=4,进而得到C(0,-1).设
BCOA,得到BC=4,进而得到C(0,-1).设![]() 的解析式为
的解析式为![]() , 把A(2,0),C(0,-1)代入即可得到
, 把A(2,0),C(0,-1)代入即可得到![]() 的解析式.
的解析式.
试题解析:(1)在Rt△AOB中,∵![]() ,∴
,∴![]() ,∴OB=3,∴点B的坐标是(0,3) .
,∴OB=3,∴点B的坐标是(0,3) .
(2)∵![]() =
=![]() BCOA,∴
BCOA,∴![]() BC×2=4,∴BC=4,∴C(0,-1).
BC×2=4,∴BC=4,∴C(0,-1).
设![]() 的解析式为
的解析式为![]() , 把A(2,0),C(0,-1)代入得:
, 把A(2,0),C(0,-1)代入得:![]() ,∴
,∴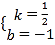 ,∴
,∴![]() 的解析式为是
的解析式为是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于概率,下列说法正确的是( )
A.莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨
B.随机抛掷一枚质地均匀的硬币,落地后一定反面向上
C.在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖
D.同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,AC=BC=4cm,D是AB的中点,以C为圆心,4cm长为半径作圆,则A,B,C,D四点中,在圆内的有( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示表示王勇同学骑自行车离家的距离与时间之间的关系,王勇9点离开家,15点回家,请结合图象,回答下列问题:
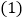 到达离家最远的地方是什么时间?离家多远?
到达离家最远的地方是什么时间?离家多远?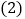 他一共休息了几次?休息时间最长的一次是多长时间?
他一共休息了几次?休息时间最长的一次是多长时间?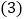 在哪些时间段内,他骑车的速度最快?最快速度是多少?
在哪些时间段内,他骑车的速度最快?最快速度是多少?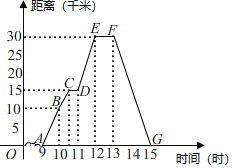
-
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y1=k1x(k1>0)与反比例函数y2=
 (k2>0)部分图象如图所示,则不等式k1x>
(k2>0)部分图象如图所示,则不等式k1x>  的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A,B,点P在该函数图象上,P到x轴、y轴的距离分别为d1,d2.
(1)当P为线段AB的中点时,d1+d2=_____;
(2)设点P横坐标为m,用含m的代数式表示d1+d2,并求当d1+d2=3时点P的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂甲、乙两车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙车间各自加工零件总数为y(件),与甲车间加工时间x(天),y与x之间的关系如图(1)所示.由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(件)与甲车间加工时间x(天)的关系如图(2)所示.

(1)甲车间每天加工零件为_____件,图中d值为_____.
(2)求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式.
(3)甲车间加工多长时间时,两车间加工零件总数为1000件?
相关试题

