【题目】如图所示,数轴上从左到右的三个点A,B,C所对应数的分别为a,b,c.其中点A、点B两点间的距离AB的长是2019,点B、点C两点间的距离BC的长是1000,
![]()
(1)若以点C为原点,直接写出点A,B所对应的数;
(2)若原点O在A,B两点之间,求|a|+|b|+|b﹣c|的值;
(3)若O是原点,且OB=19,求a+b﹣c的值.
参考答案:
【答案】(1)点A所对应的数是﹣3019,点B所对应的数﹣1000;(2)|a|+|b|+|b﹣c|=3019;(3)a+b﹣c=﹣3038或a+b﹣c=﹣3000.
【解析】
(1)根据数轴的定义可求点A,B所对应的数;
(2)先根据绝对值的性质求得|a|+|b|=2019,|bc|=1000,再代入计算即可求解;
(3)分两种情况:原点O在点B的左边;原点O在点B的右边;进行讨论即可求解.
(1)点A所对应的数是﹣1000﹣2019=﹣3019,点B所对应的数﹣1000;
(2)当原点O在A,B两点之间时,
|a|+|b|=2019,|b﹣c|=1000,
|a|+|b|+|b﹣c|=2019+1000=3019;
(3)若原点O在点B的左边,则点A,B,C所对应数分别是a=﹣2000,b=19,c=1019,
则a+b﹣c=﹣2000+19﹣1019=﹣3000;
若原点O在点B的右边,则点A,B,C所对应数分别是a=﹣2038,b=﹣19,c=981
则a+b﹣c=﹣2038+(﹣19)﹣981=﹣3038.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的顶点O在坐标原点,顶点A的坐标为(4,3)
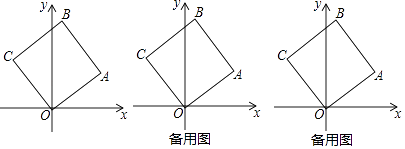
(1)顶点C的坐标为( , ),顶点B的坐标为( , );
(2)现有动点P、Q分别从C、A同时出发,点P沿线段CB向终点B运动,速度为每秒1个单位,点Q沿折线A→O→C向终点C运动,速度为每秒k个单位,当运动时间为2秒时,以P、Q、C为顶点的三角形是等腰三角形,求此时k的值.
(3)若正方形OABC以每秒 个单位的速度沿射线AO下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
个单位的速度沿射线AO下滑,直至顶点C落到x轴上时停止下滑.设正方形OABC在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“探究性学习”课中,李老师设计了如下数表:
n
2
3
4
5
…
a
22﹣1
32﹣1
42﹣1
52﹣1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)用含自然数n(n>1)的代数式表示:a,b,c.
(2)当c=101时,求n的值;
(3)用等式表示a、b、c之间的数量关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数的图像与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)一次函数的函数关系式;
(2)若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠B=90°,AB∥DF,AB=3cm,BD=8cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE.
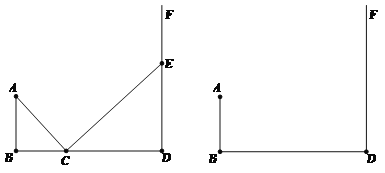
(1)试说明:∠ACB =∠CED
(2)若AC=CE ,试求DE的长
(3)在线段BD的延长线上,是否存在点C,使得AC=CE,若存在,请求出DE的长及△AEC的面积;若不存在,请说明理由。
-
科目: 来源: 题型:
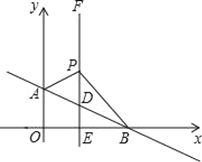
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:y=﹣
 x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
x+b交y轴于A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).(1)直线AB的表达式为__________________;
(2)①求△ABP的面积(用含n的代数式表示);
②当S△ABP=2时,求点P的坐标;
③在②的条件下,以PB为边在第一象限作等腰直角三角形BPC,请直接写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A、B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
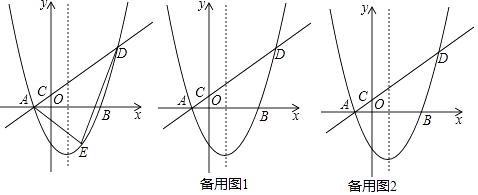
(1)直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).
(2)点E为直线l下方抛物线上一点,当△ADE的面积的最大值为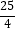 时,求抛物线的函数表达式;
时,求抛物线的函数表达式;
(3)设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.
相关试题

