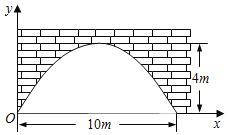
【题目】有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式;
(2)一辆宽为2米,高为3米的货船能否从桥下通过?
参考答案:
【答案】(1)抛物线解析式为y=﹣![]() x2+
x2+![]() x;(2)货船能从桥下通过.
x;(2)货船能从桥下通过.
【解析】
(1)根据题意确定抛物线顶点坐标,利用待定系数法求函数解析式;(2)由抛物线对称轴直线x=5分析,船宽2米时,计算x=6是函数值是否大于3即可求解.
(1)根据题意,得
抛物线的顶点坐标为(5,4),经过(0,0),
∴设:抛物线解析式为y=a(x﹣5)2+4,
把(0,0)代入,得
25a+4=0,解得a=![]() ,
,
所以抛物线解析式为:y=![]() (x﹣5)2+4=
(x﹣5)2+4=![]() x2+
x2+![]() x.
x.
(2)货船能从桥下通过.理由如下:
由(1)可知,抛物线对称轴为直线x=5,又∵货船宽为2米,高为3米,
∴当x=6时,y=![]() (6﹣5)2+4=3.84,
(6﹣5)2+4=3.84,
∵3.84>3,
∴货船能从桥下通过.
答:货船能从桥下通过.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在半圆O上,半径OB=2
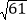 ,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A. 5B. 6C. 7D. 8
-
科目: 来源: 题型:
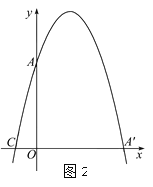
查看答案和解析>>【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.

-
科目: 来源: 题型:
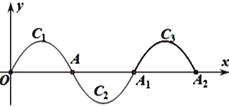
查看答案和解析>>【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:PA+PB=PC;
(2)若BC=
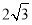 ,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.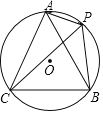
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
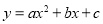 图象上部分点的横坐标
图象上部分点的横坐标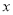 与纵坐标
与纵坐标 的对应值如表所示:
的对应值如表所示:
···
-3
-2
-1
0
···

···
0
-3
-4
-3
···
直接写出不等式
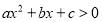 的解集是____________________.
的解集是____________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
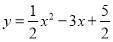 ,
,(1)该二次函数图象与x轴的交点坐标是______________;
(2)将
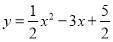 化成
化成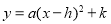 的形式_____________________,并写出顶点坐标______________.
的形式_____________________,并写出顶点坐标______________.(3)在坐标轴中画出此抛物线的大致图象;
(4)写出不等式
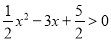 的解集___________________;
的解集___________________;
(5)当
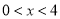 时,直接写出y的取值范围_________________.
时,直接写出y的取值范围_________________.
相关试题

