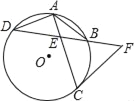
【题目】如图,点D在半圆O上,半径OB=2![]() ,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )

A. 5B. 6C. 7D. 8
参考答案:
【答案】D
【解析】
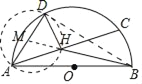
如图,取AD的中点M,连接BD,HM,BM.由题意点H在以M为圆心,MD为半径的⊙M上,推出当M、H、B共线时,BH的值最小;
解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD=![]() =12,
=12,
BM=![]() =13,
=13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在
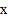 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
-
科目: 来源: 题型:
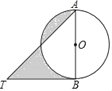
查看答案和解析>>【题目】如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,⊙O中,弦AC、BD交于E,
 .
.(1)求证:
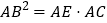 ;
;(2)延长EB到F,使EF=CF,试判断CF与⊙O的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
(1)求证:△ADB≌△CDE;
(2)求∠MDN的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 都在反比例函数
都在反比例函数 的图象上.
的图象上.(1)求
 的值;
的值;(2)如果
 为
为 轴上一点,
轴上一点, 为
为 轴上一点,以点
轴上一点,以点 为顶点的四边形是平行四边形,试求直线
为顶点的四边形是平行四边形,试求直线 的函数表达式;
的函数表达式;(3)将线段
 沿直线
沿直线 进行对折得到线段
进行对折得到线段 ,且点
,且点 始终在直线
始终在直线 上,当线段
上,当线段 与
与 轴有交点时,则
轴有交点时,则 的取值范围为_______(直接写出答案)
的取值范围为_______(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校两次购买足球和篮球的支出情况如表:
足球(个)
篮球(个)
总支出(元)
第一次
2
3
310
第二次
5
2
500
(1)求购买一个足球、一个篮球的花费各需多少元?(请列方程组求解)
(2)学校准备给帮扶的贫困学校送足球、篮球共计60个,恰逢市场对两种球的价格进行了调整,足球售价提高了10%,篮球售价降低了10%,如果要求一次性购得这批球的总费用不超过4000元,那么最多可以购买多少个足球?
相关试题

