搜索
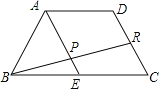
【题目】如图，AD∥BC，BC=2AD，E为BC的中点，R为DC的中点，BR交AE于点P，则EP：AP= ．
参考答案：
【答案】
．
【解析】
试题分析：先由BC=2AD，BE=EC=
BC，得出BE=EC=AD，根据AD∥BC，由一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形，那么EA=CD，EA∥CD．得出△BEP∽△BCR，于是EP=CR，而CR=CD，那么EP=
CD=EA，然后根据比例的性质即可求出答案即可．
解：∵BC=2AD，BE=EC=BC，
∴BE=EC=AD，
∵在等腰梯形ABCD中，AD∥BC，
∴四边形ADCE是平行四边形，
∴EA=CD，EA∥CD，
∴△BEP∽△BCR，
∵BE=EC=BC，
∴EP=
CR，
∵CR=CD，
∴EP=
CD=EA，
∴
=，
∴EP：AP=．
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【观察发现】
如图1，四边形ABCD和四边形AEFG都是正方形，且点E在边AB上，连接DE和BG，猜想线段DE与BG的数量关系，以及直线DE与直线BG的位置关系．（只要求写出结论，不必说出理由）
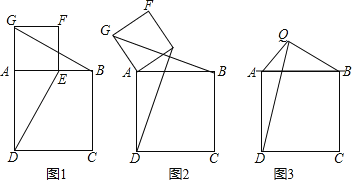
【深入探究】
如图2，将图1中正方形AEFG绕点A逆时针旋转一定的角度，其他条件与观察发现中的条件相同，观察发现中的结论是否还成立？请根据图2加以说明．
【拓展应用】
如图3，直线l上有两个动点A、B，直线l外有一点O，连接OA，OB，OA，OB长分别为
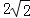、4，以线段AB为边在l的另一侧作正方形ABCD，连接OD．随着动点A、B的移动，线段OD的长也会发生变化，在变化过程中，线段OD的长是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由． -
科目： 来源： 题型：
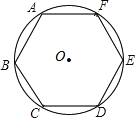
查看答案和解析>>【题目】如图，正六边形ABCDEF内接于⊙O，向⊙O内任意投点，则所投的点落在正六边形ABCDEF内的概率是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】等腰三角形ABC内接于圆O，AB=AC，AB的垂直平分线MN与边AB交于点M，与AC所在的直线交于点N，若∠ANM=70°，则劣弧
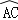所对的圆心角的度数为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为原点，线段AB的两个端点A（0，2），B（1，0）分别在y轴和x轴的正半轴上，点C为线段AB的中点，现将线段BA绕点B按顺时针方向旋转90°得到线段BD，连结CD，某抛物线y=ax2+bx+c（a≠0）经过点D、点E（1，1）．
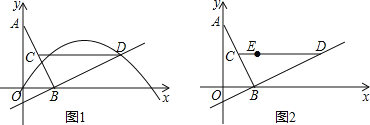
（1）若该抛物线过原点O，则a= ；
（2）若点Q在抛物线上，且满足∠QOB与∠BCD互余，要使得符合条件的Q点的个数是4个，则a的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一个多边形的内角和为540°，则这个多边形的边数为( )
A. 3 B. 4 C. 5 D. 6
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图1，二次函数y=ax2﹣2ax+c（a＞0）的图象与y轴交于点C（0，﹣4），与x轴交于点A、B两点，点A的坐标为（4，0）．
（1）求该抛物线的函数解析式；
（2）点P（t，0）是线段OB上一动点（不与O、B重合），点E是线段BC上的点，以点B、P、E为顶点的三角形与三角形ABC相似，连结CP，求△CPE的面积S与t的函数关系式；
（3）如图2，若平行于x轴的动直线与该抛物线交于点Q，与直线AC交于点F，点D的坐标为（2，0），则存在这样的直线，使得△ODF为等腰三角形，请直接写出点Q坐标．
相关试题
