【题目】已知:如图1,二次函数y=ax2﹣2ax+c(a>0)的图象与y轴交于点C(0,﹣4),与x轴交于点A、B两点,点A的坐标为(4,0).

(1)求该抛物线的函数解析式;
(2)点P(t,0)是线段OB上一动点(不与O、B重合),点E是线段BC上的点,以点B、P、E为顶点的三角形与三角形ABC相似,连结CP,求△CPE的面积S与t的函数关系式;
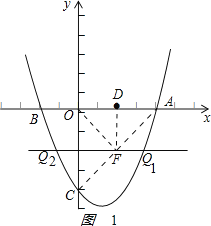
(3)如图2,若平行于x轴的动直线与该抛物线交于点Q,与直线AC交于点F,点D的坐标为(2,0),则存在这样的直线,使得△ODF为等腰三角形,请直接写出点Q坐标.
参考答案:
【答案】(1)y=![]() x2﹣x﹣4;(2)S=﹣
x2﹣x﹣4;(2)S=﹣![]() t2﹣
t2﹣![]() t+
t+![]() ;(3)存在这样的直线l,使得△ODF是等腰三角形,点Q的坐标为:Q1(1+
;(3)存在这样的直线l,使得△ODF是等腰三角形,点Q的坐标为:Q1(1+![]() ,﹣2)或Q2(1﹣
,﹣2)或Q2(1﹣![]() ,﹣2)或Q3(1+
,﹣2)或Q3(1+![]() ,﹣3)或Q4(1﹣
,﹣3)或Q4(1﹣![]() ,﹣3).
,﹣3).
【解析】
试题分析:(1)根据待定系数法,可得函数解析式;
(2)可先设P的坐标为(m,0);根据相似三角形的性质,可得S△BEP,根据S△CPE=S△BOC﹣S△BPE﹣SOPC,可得函数关系式;
(3)本题要分三种情况进行求解:①当OD=OF时,根据等腰直角三角形,可得出F的坐标应该是(2,2),根据F的纵坐标代入抛物线的解析式中即可求出Q的坐标;②当OF=DF时,根据线段垂直平分线的性质,可得OM=1,根据等腰直角三角形的性质,可得FM=AM=3,也就得出了F的纵坐标,根据①的方法求出Q的坐标;③当OD=OF时,OF=2,由于O到AC的最短距离为2![]() ,因此此种情况是不成立的,综合上面的情况即可得出符合条件的P的坐标
,因此此种情况是不成立的,综合上面的情况即可得出符合条件的P的坐标
解:(1)把C(0,﹣4)和A(4,0)代入y=ax2﹣2ax+c(a>0)得,
![]() ,解得
,解得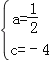
解析式为y=![]() x2﹣x﹣4;
x2﹣x﹣4;
(2)BP=t+2,OP=﹣t,S△ABC=4×6÷2=12,S△OPC=4×(﹣t)÷2=2t,
①△BPE∽△BAC,则![]() =
=![]() ,
,
则![]() =(
=(![]() )2,S△BPE=(
)2,S△BPE=(![]() )2×12=
)2×12=![]()
S△CPE=S△BOC﹣S△BPE﹣SOPC=4﹣![]() ﹣(﹣2t)=﹣
﹣(﹣2t)=﹣![]() t2+
t2+![]() t+
t+![]()
②△BEP∽△BAC,则![]() =
=![]() ,
,
则![]() =(
=(![]() )2,S△BEP=(
)2,S△BEP=(![]() )2×12=
)2×12=![]()
S△CPE=S△BOC﹣S△BPE﹣SOPC=4﹣![]() ﹣(﹣2t)=﹣
﹣(﹣2t)=﹣![]() t2﹣
t2﹣![]() t+
t+![]()
(3)存在这样的直线,使得△ODF是等腰三角形,理由为:
在△ODF中,分三种情况考虑:
①若DO=DF,如图1:
 ,
,
∵A(4,0),D(2,0),
∴AD=OD=DF=2,
又在Rt△AOC中,OA=OC=4,
∴∠OAC=45°,
∴∠DFA=∠OAC=45°,
∴∠ADF=90°,
此时,点F的坐标为(2,﹣2),
由![]() x2﹣x﹣4=﹣2,
x2﹣x﹣4=﹣2,
解得:x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,
,
此时,点P的坐标为:P(1+![]() ,﹣2)或P(1﹣
,﹣2)或P(1﹣![]() ,﹣2);
,﹣2);
②若FO=FD,过点F作FM⊥x轴于点M,如图2:
 ,
,
由等腰三角形的性质得:OM=![]() OD=1,
OD=1,
∴AM=3,
∴在等腰直角△AMF中,MF=AM=3,
∴F(1,3),
由![]() x2﹣x﹣4=﹣3,
x2﹣x﹣4=﹣3,
解得:x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,
,
此时,点P的坐标为:P(1+![]() ,﹣3)或P(1﹣
,﹣3)或P(1﹣![]() ,﹣3);
,﹣3);
③若OD=OF,
∵OA=OC=4,且∠AOC=90°,
∴AC=4 ![]() ,
,
∴点O到AC的距离为2√2,而OF=OD=2<2√2,与OF≥2√2矛盾,
所以AC上不存在点使得OF=OD=2,
此时,不存在这样的直线l,使得△ODF是等腰三角形;
综上所述,存在这样的直线l,使得△ODF是等腰三角形,点Q的坐标为:Q1(1+![]() ,﹣2)或Q2(1﹣
,﹣2)或Q2(1﹣![]() ,﹣2)或Q3(1+
,﹣2)或Q3(1+![]() ,﹣3)或Q4(1﹣
,﹣3)或Q4(1﹣![]() ,﹣3).
,﹣3).
-
科目: 来源: 题型:
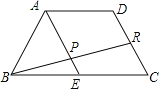
查看答案和解析>>【题目】如图,AD∥BC,BC=2AD,E为BC的中点,R为DC的中点,BR交AE于点P,则EP:AP= .
-
科目: 来源: 题型:
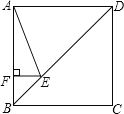
查看答案和解析>>【题目】如图,O为原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,连结CD,某抛物线y=ax2+bx+c(a≠0)经过点D、点E(1,1).
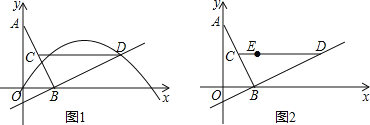
(1)若该抛物线过原点O,则a= ;
(2)若点Q在抛物线上,且满足∠QOB与∠BCD互余,要使得符合条件的Q点的个数是4个,则a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和为540°,则这个多边形的边数为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A.1 B.
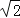 C.4﹣2
C.4﹣2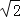 D.3
D.3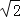 ﹣4
﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,P点在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+n.
(1)当销售单价x定为25元时,李明每月获得利润为w为1250元,则n= ;
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)当销售单价定为多少元时,每月可获得最大利润?并求最大利润为多少元.
相关试题

