【题目】填空完成推理过程:
如图,BCE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证AD∥BE.

证明:∵AB∥CD(已知)
∴∠4=∠BAE( )
∵∠3=∠4(已知)
∴∠3=∠ (等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即∠BAF=∠CAD
∴∠3=∠ (等量代换)
∴AD∥BE( )
参考答案:
【答案】两直线平行,同位角相等;BAE;等式的性质;DAC;内错角相等,两直线平行.
【解析】
根据已知条件和解题思路,利用平行线的性质和判定填空.
解:AD∥BE,理由如下:
∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等);
∵∠3=∠4(已知),
∴∠3=∠BAE(等量代换);
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质),
即∠BAF=∠DAC,
∴∠3=∠DAC(等量代换),
∴AD∥BE(内错角相等,两直线平行).
故答案是:两直线平行,同位角相等;BAE;等式的性质;DAC;内错角相等,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____,使△AEH≌△CEB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
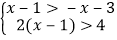
(1)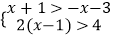
(2)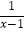 +1=
+1= 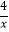 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABED是正方形,DB⊥BC,点E为线段DC的中点,
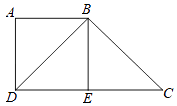
(1)求证:BD2=ADDC.
(2)连接AE,求证:ABCE为平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,有点P(a,b),实数a,b,m满足以下两个等式:
2a﹣3m+1=0,3b﹣2m﹣16=0
(1)当a=1时,点P到x轴的距离为 ;
(2)若点P落在x轴上,点P平移后对应点为P′(a+15,b+4),求点P和P′的坐标;
(3)当a≤4<b时,求m的最小整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+2)x+m=0,
(1)求证:无论m取何值,原方程总有两个不相等的实数根.
(2)若x1 , x2是原方程的两根,且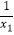 +
+  =﹣2,求m的值.
=﹣2,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )

A. 3B. 4C. 5D. 6
相关试题

