【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°.点D是直线BC上的一个动点,连接AD,并以AD为边在AD的右侧作等边△ADE.
(1)如图①,当点E恰好在线段BC上时,请判断线段DE和BE的数量关系,并结合图①证明你的结论;
(2)当点E不在直线BC上时,连接BE,其它条件不变,(1)中结论是否成立?若成立,请结合图②给予证明;若不成立,请直接写出新的结论;
(3)若AC=3,点D在直线BC上移动的过程中,是否存在以A、C、D、E为顶点的四边形是梯形?如果存在,直接写出线段CD的长度;如果不存在,请说明理由.
参考答案:
【答案】
(1)
解:DE=BE.理由如下:
∵△ADE为等边三角形,
∴AD=DE=AE,∠AED=60°.
∵∠ABC=30°,∠AED=∠ABC+∠EAB,
∴∠EAB=60°﹣30°=30°,
∴∠ABC=∠EAB,
∴EB=AE,
∴EB=DE;
(2)
解:如图,
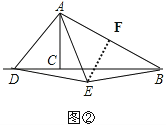
过点E作EF⊥AB,垂足为F,
在△ABC中,∠ABC=30°,
∴∠CAB=60°,
∴∠DAE=∠CAB,
∴∠DAE﹣∠CAE=∠BAC﹣∠CAE,
则∠CAD=∠EAF.
又∵AD=AE,∠ACD=∠AFE,
∴△ADC≌△AEF,
∴AC=AF.
在△ABC中,∠ABC=30°,
∴AC= ![]() AB,
AB,
∴AF=BF,
∴EA=EB,
∴DE=EB;
(3)
解:如图,
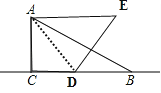
∵四边形ACDE是梯形,∠ACD=90°,
∴∠CAE=90°.
∵∠CAE=∠CAD+∠EAD,
又∵在正三角形ADE中,∠EAD=60°,
∴∠CAD=30°.
在直角三角形ACD中,AC=3,∠CAD=30°,
由勾股定理可得CD= ![]() .
.
同理可得:若点D与点B重合,AC平行DE,此时CD=3 ![]() ,
,
综上所述:若AE∥CD,CD= ![]() ;若点D与点B重合,此时CD=3
;若点D与点B重合,此时CD=3 ![]()
【解析】(1)利用等边三角形的性质以及等腰三角形的判定解答即可;(2)过点E作EF⊥AB,垂足为F,证得△ADC≌△AEF,结合直角三角形中30度的角所对的直角边是斜边的一半解决问题;(3)从A、C、D、E为顶点的梯形的性质入手,逐步找出解决问题的方案.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生孝敬父母的情况(选项:A为父母洗一次脚;B帮父母做一次家务;C给父母买一件礼物;D其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
根据以上信息解答下列问题:


(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小梅将边长分别为
 ,
, ,
, ,
, ,
, ,
, …长的若干个正方形按一定规律拼成不同的长方形,如图所示.
…长的若干个正方形按一定规律拼成不同的长方形,如图所示. 求第四个长方形的周长;
求第四个长方形的周长; 当
当 时,求第五个长方形的面积.(用科学记数法表示)
时,求第五个长方形的面积.(用科学记数法表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点
 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米): ,
, ,
, ,
, ,
, ,
, ,
, .
. 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点 .
. 蜗牛离开出发点
蜗牛离开出发点 最远时是多少厘米?
最远时是多少厘米? 在爬行过程中,如果每爬
在爬行过程中,如果每爬 厘米奖励
厘米奖励 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
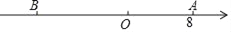
-
科目: 来源: 题型:
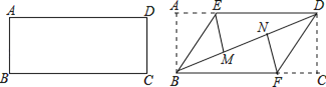
查看答案和解析>>【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形.
(2)若四边形BFDE是菱形,BE =2,求菱形BFDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.
试问:(1)规定日期是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
相关试题

