【题目】如图,直线y=x和直线y=﹣x+5相交于点M,直线PQ⊥x轴,分别交直线y=﹣x+5和直线y=x于点P、Q,点R是y轴上一点,若△PQR为等腰直角三角形.求点R的坐标.

参考答案:
【答案】点R的坐标是(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() )或(0,5)或(0,0).
)或(0,5)或(0,0).
【解析】
首先求出PQ的长,分五种情况进行讨论:①如图1,当PR=PQ时,△PQR为等腰直角三角形,根据PQ=PR列方程求得;②如图2,当RQ=PQ时,△PQR为等腰直角三角形,根据PQ=RQ列方程求得;③如图3,当∠PRQ=90°时,△PQR为等腰直角三角形,根据2RB=PQ列方程求得;④⑤P在M的右侧,同理可得R的坐标.
解:设直线PQ的解析式为:x=h,
∴P(h,﹣h+5)、Q(h,h),
∴PQ=﹣h+5﹣h=5﹣2h,
分三种情况:
①如图1,过P作PR⊥y轴于R,连接RQ,

当PR=PQ时,△PQR为等腰直角三角形,
∴h=5﹣2h,
h=![]() ,
,
∴﹣h+5=﹣![]() +5=
+5=![]() ,
,
∴R(0,![]() );
);
②如图2,过Q作QR⊥y轴于R,连接RP,
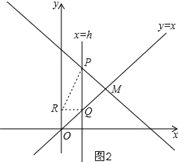
当RQ=PQ时,△PQR为等腰直角三角形,
∴h=5﹣2h,
h=![]() ,
,
∴R(0,![]() );
);
③如图3,作线段PQ的中垂线l,交y轴于R,交PQ于B,连接PR、RQ,则PR=RQ,

当∠PRQ=90°时,△PQR为等腰直角三角形,
∴∠PRB=∠QRB=45°,
∴△PBR和△BRQ都是等腰直角三角形,
∴2RB=2BQ=PQ,
则2h=5﹣2h,
h=![]() ,
,
∴OR=![]() +
+![]() (5﹣2h)=
(5﹣2h)=![]() +
+![]() ﹣
﹣![]() =
=![]() ,
,
∴R(0,![]() );
);
④如图4,P在交点M的右侧时,QR=QP,
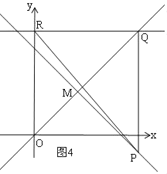
则h=h﹣(﹣h+5),
h=5,
∴R(0,5),
如图5,P在交点M的右侧时,QP=RP,
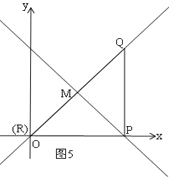
同理可得R(0,0),此时R与原点重合,
综上所述,若△PQR为等腰直角三角形.点R的坐标是(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() )或(0,5)或(0,0).
)或(0,5)或(0,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求不等式4(x+1)≤24的正整数解;
(2)解不等式
 x-1≤
x-1≤ x-
x- ,把它的解集在数轴上表示出来,并求出这个不等式的负整数解.
,把它的解集在数轴上表示出来,并求出这个不等式的负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
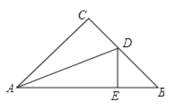
A. 4cm B. 6cm C. 8cm D. 10cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2,点A、D在l1上,AB⊥l1,CD⊥l2,垂足分别是B、C,点E,F在l2上,AE∥DF,那么AE与DF、BE与CF相等吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,过点C作CE⊥AB于点E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=
 (AB+AD).
(AB+AD).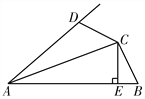
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,己知点
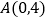 ,
,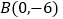 ,
,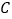 是x轴上的一个动点,当
是x轴上的一个动点,当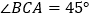 时,点
时,点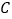 的坐标为__________.
的坐标为__________.
相关试题

