【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
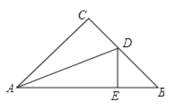
A. 4cm B. 6cm C. 8cm D. 10cm
参考答案:
【答案】B
【解析】试题解析:∵AD平分∠CAB交BC于点D
∴∠CAD=∠EAD
∵DE⊥AB
∴∠AED=∠C=90
∵AD=AD
∴△ACD≌△AED.(AAS)
∴AC=AE,CD=DE
∵∠C=90°,AC=BC
∴∠B=45°
∴DE=BE
∵AC=BC,AB=6cm,
∴2BC2=AB2,即BC=![]() ,
,
∴BE=AB-AE=AB-AC=6-3![]() ,
,
∴BC+BE=3![]() +6-3
+6-3![]() =6cm,
=6cm,
∵△DEB的周长=DE+DB+BE=BC+BE=6(cm).
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,将正方形的边AD绕点A顺时针旋转到AE,连接BE、DE,过点A作AF⊥BE于F,交直线DE于P.
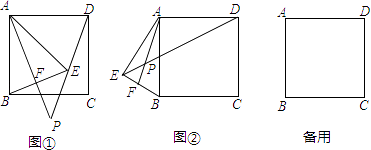
(1)如图①,若∠DAE=40°,求∠P的度数;
(2)如图②,若90°<∠DAE<180°,其它条件不变,试探究线段AP、DP、EP之间的数量关系,并说明理由;
(3)继续旋转线段AD,若旋转角180°<∠DAE<270°,则线段AP、DP、EP之间的数量关系为(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
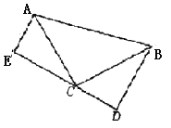
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系。
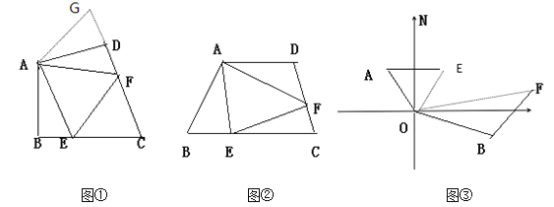
(1)小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,即可得出BE,EF,FD之间的数量关系,他的结论应是____________。
象上面这样有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等的几何模型称为半角模型。
(2)拓展 如图②,若在四边形ABCD中,,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=
 ∠BAD,则BE,EF,FD之间的数量关系是________________。
∠BAD,则BE,EF,FD之间的数量关系是________________。请证明你的结论。
(3)实际应用 如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西35°的A处,舰艇乙在指挥中心南偏东75°的B处,,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为65°,试求此时两舰艇之间的距离是_____________海里 (直接写出答案)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间可供游客居住,当每个房间每天的定价为180元时,房间会全部住满,当每个房间每天的定价增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间的定价增加x元(x为10的整数倍),此时入住的房间数为y间,宾馆每天的利润为w元.
(1)直接写出y(间)与x(元)之间的函数关系;
(2)如何定价才能使宾馆每天的利润w(元)最大?
(3)若宾馆每天的利润为10800元,则每个房间每天的定价为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D为BC上一点,以AD为腰作等腰△ADE,AD=AE,∠BAC=∠DAE,连接CE.
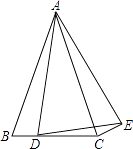
(1)求证:BD=CE;
(2)已知BC=8,∠BAC=∠DAE=30°,若△DCE的面积为1,求线段BD的长.
相关试题

