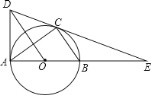
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)、求证:DE是⊙O的切线;(2)、若AE=6,CE=![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
参考答案:
【答案】(1)、证明过程见解析;(2)、2![]() .
.
【解析】
试题分析:(1)、连接OC得出∠AOD=∠COD,证明△AOD和△COD全等得出切线;(2)、根据Rt△OCE的勾股定理求出半径,然后得出∠COE的度数,然后求出扇形COB的面积,从而得出所求图形的面积.
试题解析:(1)、连结OC,证得∠AOD=∠COD ;证得△AOD≌△COD(SAS); 证得∠OCD=∠OAD=90°;
则DE是⊙O的切线.
(2)、设半径为r,在Rt△OCE中,OC2+CE2=OE2 ![]() 解得
解得![]()
![]()
![]()
![]() 所求图形面积为
所求图形面积为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处。
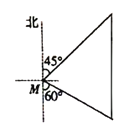
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时)。(参考数据:
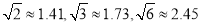 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程m
 -(m+2)x+2=0有两个不相等的实数根
-(m+2)x+2=0有两个不相等的实数根 ,
,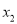 .
.(1)、求m的取值范围;
(2)、若
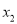 <0,且
<0,且 >-1,求整数m的值.
>-1,求整数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a和b是有理数,若a+b=0,a2+b2≠0,则在a和b之间一定( )
A. 存在负整数 B. 存在正整数 C. 存在一个正数和负数 D. 不存在正分数
-
科目: 来源: 题型:
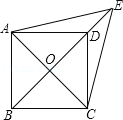
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
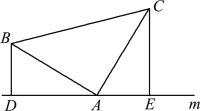
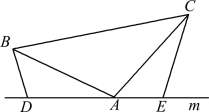
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,与y轴的交于C点,其中A点的坐标为(-3,0).

(1)求抛物线的表达式;
(2)若将此抛物线向右平移m个单位,A、B、C三点在坐标轴上的位置也相应的发生移动,在移动过程中,△BOC能否成为等腰直角三角形?若能,求出m的值,若不能,请说明理由.
相关试题

