【题目】如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,与y轴的交于C点,其中A点的坐标为(-3,0).

(1)求抛物线的表达式;
(2)若将此抛物线向右平移m个单位,A、B、C三点在坐标轴上的位置也相应的发生移动,在移动过程中,△BOC能否成为等腰直角三角形?若能,求出m的值,若不能,请说明理由.
参考答案:
【答案】(1)、![]() ;(2)、m=2或m=4.
;(2)、m=2或m=4.
【解析】
试题分析:(1)、根据A点和对称轴求出点B的坐标,然后利用待定系数法进行求解;(2)、首先根据题意得出B、C的点坐标,然后进行计算.
试题解析:(1)、根据题意得:B(1,0) 将A、B代入求得:![]()
(2)、平移后B(m+1,0),C(0,m2-2m-3)
①m2-2m-3=-(m+1),解得m=2,m=1舍去; ②m2-2m-3=m+1,解得m=4,m=1舍去;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)、求证:DE是⊙O的切线;(2)、若AE=6,CE=
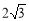 ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)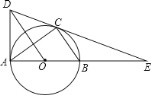
-
科目: 来源: 题型:
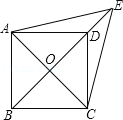
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
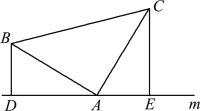
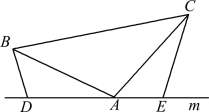
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把直线y=-x-1沿x轴向右平移2个单位,所得直线的函数解析式为( )
A. y=-x+1B. y=-x-3C. y=-2x-1D. y=2x-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣1,5),将点A向右平移2个单位,再向下平移3个单位得到点A1;点A1关于y轴与A2对称,则A2的坐标为( )
A.(2,﹣1)
B.(1,2)
C.(﹣1,2)
D.(﹣2,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】在体育课的跳远比赛中,以5.00米为标准,若小东跳出了5.22米,可记做+0.22,那么小东跳出了4.85米,记作 .
相关试题

