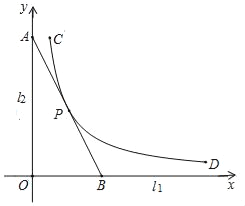
【题目】如图,直线l1,l2是紧靠某湖泊的两条相互垂直的公路,曲线段CD是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路AB,用以连接两条公路和环湖观光大道,且直线AB与曲线段CD有且仅有一个公共点P.已知点C到l1,l2的距离分别为8km和1km,点P到l1的距离为4km,点D到l1的距离为0.8km.若分别以l1,l2为x轴、y轴建立平面直角坐标系xOy,则曲线段CD对应的函数解析式为y=![]() .
.
(1)求k的值,并指出函数y=![]() 的自变量的取值范围;
的自变量的取值范围;
(2)求直线AB的解析式,并求出公路AB长度(结果保留根号).
参考答案:
【答案】(1)k=8,1≤x≤10;(2)4![]() km.
km.
【解析】试题分析:![]() 写出点C的坐标,把点C的坐标代入反比例函数即可求得反比例函数的解析式,进而根据点
写出点C的坐标,把点C的坐标代入反比例函数即可求得反比例函数的解析式,进而根据点![]() 的纵坐标求得点
的纵坐标求得点![]() 的横坐标,即可写出自变量的取值范围.
的横坐标,即可写出自变量的取值范围.
![]() 先求出直线
先求出直线![]() 的解析式,求出点
的解析式,求出点![]() 的坐标,即可求出公里
的坐标,即可求出公里![]() 的长度.
的长度.
试题解析:(1)由题意得,点C的坐标为![]()
将其代入![]() 得,
得,![]()
∴曲线段CD的函数解析式为![]()
∴点D的坐标为![]()
∴自变量的取值范围为![]()
(2)设直线AB的解析式为![]()
由(1)易求得点P的坐标为![]()
![]() 即
即![]()
∴直线AB的解析式为![]()
联立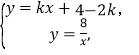
得![]()
![]()
∴由题意得,![]()
解得![]()
∴直线AB的解析式为![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
即![]() 的坐标分别为
的坐标分别为![]()
![]()
∴公路AB的长度为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
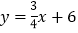 的图象与
的图象与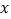 ,
,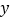 轴分别交于
轴分别交于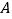 ,
,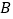 两点,点
两点,点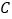 与点
与点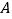 关于
关于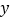 轴对称.动点
轴对称.动点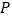 ,
,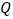 分别在线段
分别在线段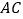 ,
,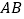 上(点
上(点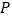 与点
与点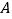 ,
,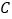 不重合),且满足
不重合),且满足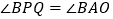 .
.(1)求点
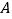 ,
,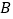 的坐标及线段
的坐标及线段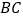 的长度;
的长度;(2)当点
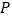 在什么位置时,
在什么位置时,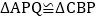 ,说明理由;
,说明理由;(3)当
 为等腰三角形时,求点
为等腰三角形时,求点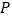 的坐标.
的坐标.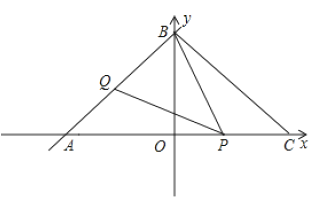
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A.
 B.
B.  C. 3 D.
C. 3 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
-
科目: 来源: 题型:
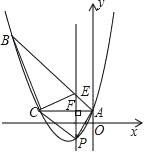
查看答案和解析>>【题目】如图,已知抛物线y=
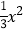 +bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点的坐标分别为(6,0),(0,6),点P从点A出发,沿AB方向以每秒
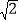 个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.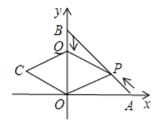
相关试题

