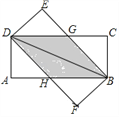
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置，BD为重合的对角线．重叠部分为四边形DHBG．

（1）试判断四边形DHBG为何种特殊的四边形，并说明理由；

（2）若AB＝8，AD＝4，求四边形DHBG的面积．

参考答案：

【答案】（1）四边形DHBG是菱形，理由见解析；（2）20．

【解析】解：（1）四边形DHBG是菱形．

理由如下：

∵四边形ABCD、FBED是完全相同的矩形，

∴∠A=∠E=90°，AD=ED，AB=EB．

∴△DAB≌△DEB（SAS），

∴∠ABD=∠EBD．

∵AB∥CD，DF∥BE，

∴四边形DHBG是平行四边形，∠HDB=∠EBD，

∴∠HDB=∠HBD，

∴DH=BH，

∴四边形DHBG是菱形．

（2）由（1），设DH=BH=x，则AH=8x，

在Rt△ADH中，AD +AH =DH ，即4 +（8x）=x ，

解得：x=5，即BH=5，

∴菱形DHBG的面积为HBAD=5×4=20．

关闭