【题目】如图,一次函数![]() 的图象与
的图象与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.动点
轴对称.动点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上(点
上(点![]() 与点
与点![]() ,
,![]() 不重合),且满足
不重合),且满足![]() .
.
(1)求点![]() ,
,![]() 的坐标及线段
的坐标及线段![]() 的长度;
的长度;
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由;
,说明理由;
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
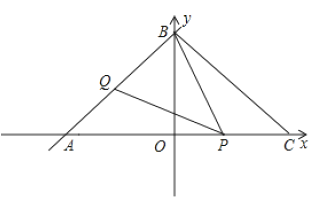
参考答案:
【答案】(1)10;(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点![]() ,
,![]() 的坐标,结合点
的坐标,结合点![]() 与点
与点![]() 关于
关于![]() 轴对称可得出点
轴对称可得出点![]() 的坐标,进而可得出线段
的坐标,进而可得出线段![]() 的长度;
的长度;
(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ,由点
,由点![]() ,
,![]() 的坐标可得出
的坐标可得出![]() 的长度,由勾股定理可求出
的长度,由勾股定理可求出![]() 的长度,进而可得出
的长度,进而可得出![]() ,通过角的计算及对称的性质可得出
,通过角的计算及对称的性质可得出![]() ,
,![]() ,结合
,结合![]() 可证出
可证出![]() ,由此可得出:当点
,由此可得出:当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ;
;
(3)分![]() ,
,![]() 及
及![]() 三种情况考虑:①当
三种情况考虑:①当![]() 时,由(2)的结论结合全等三角形的性质可得出当点
时,由(2)的结论结合全等三角形的性质可得出当点![]() 的坐标是
的坐标是![]() 时
时![]() ;②当
;②当![]() 时,利用等腰三角形的性质结合
时,利用等腰三角形的性质结合![]() 可得出
可得出![]() ,利用三角形外角的性质可得出
,利用三角形外角的性质可得出![]() ,进而可得出此种情况不存在;③当
,进而可得出此种情况不存在;③当![]() 时,利用等腰三角形的性质结合
时,利用等腰三角形的性质结合![]() 可得出
可得出![]() ,设此时
,设此时![]() 的坐标是
的坐标是![]() ,在
,在![]() 中利用勾股定理可得出关于
中利用勾股定理可得出关于![]() 的一元一次方程,解之即可得出结论.综上,此题得解.
的一元一次方程,解之即可得出结论.综上,此题得解.
解:(1)当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() .
.
(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ,理由如下:
,理由如下:
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]()
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 和
和![]() 关于
关于![]() 轴对称,
轴对称,
![]() .
.
在![]() 和
和![]() 中
中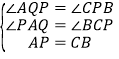 ,
,
![]() .
.
![]() 当点
当点![]() 的坐标是
的坐标是![]() 时,
时,![]() .
.
(3)分为三种情况:
①当![]() 时,如图1所示,由(2)知,当点
时,如图1所示,由(2)知,当点![]() 的坐标是
的坐标是![]() 时,
时,
![]()
![]() ,
,
![]() 此时
此时![]() 点的坐标是
点的坐标是![]() ;
;
②当![]() 时,则
时,则![]() ,
,
![]() ,
,
![]() .
.
而根据三角形的外角性质得:![]() ,
,
![]() 此种情况不存在;
此种情况不存在;
③当![]() 时,则
时,则![]() ,
,
![]() ,如图2所示.
,如图2所示.
设此时![]() 的坐标是
的坐标是![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 此时
此时![]() 的坐标是
的坐标是![]() .
.
综上所述:当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料阅读:如图①所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
解决问题:
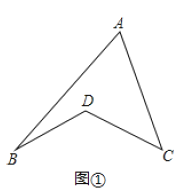
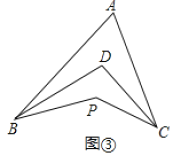
(1)观察“规形图”,试探究
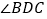 与
与 ,
, ,
,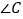 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下两个问题:
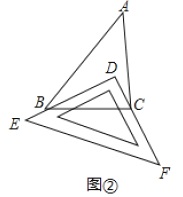
Ⅰ.如图②,把一块三角尺
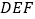 放置在
放置在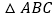 上,使三角尺的两条直角边
上,使三角尺的两条直角边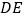 ,
,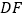 恰好经过点
恰好经过点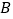 ,
,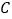 ,若
,若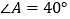 ,则
,则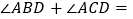 _____
_____ .
.Ⅱ.如图③,
 平分
平分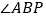 ,
,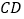 平分
平分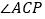 ,若
,若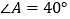 ,
,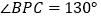 ,求
,求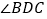 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接2022年北京冬奥会,萍乡外国语学校组织了一次大型长跑比赛。甲,乙两人在比赛时,路程
 (米)与时间
(米)与时间 (分钟)的关系如图所示,极据图像解答下列问题:
(分钟)的关系如图所示,极据图像解答下列问题:
(1)这次长跑比赛的全程是___米;先到达终点的人比另一个人领先____分钟:
(2)乙是学校田径队运动员,十分注意比赛技巧,比赛过程分起跑、途中跑冲刺跑三阶段,经历了两次加速过程.问第
 分钟时乙还落后甲多少米?
分钟时乙还落后甲多少米?(3)假设乙在第一次加速后,始终保持这个速度继续前进。那么甲,乙两人谁先到达终点?请说明理由.
(4)事实上乙追上甲的时间是多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A.
 B.
B.  C. 3 D.
C. 3 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
-
科目: 来源: 题型:
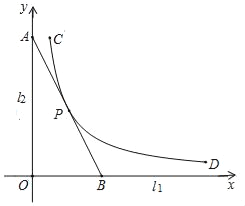
查看答案和解析>>【题目】如图,直线l1,l2是紧靠某湖泊的两条相互垂直的公路,曲线段CD是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路AB,用以连接两条公路和环湖观光大道,且直线AB与曲线段CD有且仅有一个公共点P.已知点C到l1,l2的距离分别为8km和1km,点P到l1的距离为4km,点D到l1的距离为0.8km.若分别以l1,l2为x轴、y轴建立平面直角坐标系xOy,则曲线段CD对应的函数解析式为y=
 .
.(1)求k的值,并指出函数y=
 的自变量的取值范围;
的自变量的取值范围;(2)求直线AB的解析式,并求出公路AB长度(结果保留根号).
相关试题

