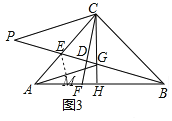
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE,CG平分∠ACB交BD于点G,
(1)如图1,求证:CF=BG;
(2)如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
求证:PB=CP+CF;
(3)如图3,在(2)间的条件下,当∠GAC=2∠FCH时,若S△AEG=3![]() ,BG=6,求AC的长.
,BG=6,求AC的长.

参考答案:
【答案】(1)见详解;(2)见详解;(3)3![]() +3
+3
【解析】
(1)根据ASA证明△BCG≌△CAF,则CF=BG;
(2)先证明△ACG≌△BCG,得∠CAG=∠CBE,再证明∠PCG=∠PGC,即可得出结论;
(3)作△AEG的高线EM,根据角的大小关系得出∠CAG=30°,根据面积求出EM的长,利用30°角的三角函数值依次求AE、EG、BE的长,所以CE=3+![]() ,根据线段的和得出AC的长.
,根据线段的和得出AC的长.
解::(1)∵∠ACB=90°,AC=BC,
∴∠A=45°,
∵CG平分∠ACB,
∴∠ACG=∠BCG=45°,
∴∠A=∠BCG,
在△BCG和△CAF中,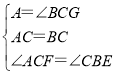 ,
,
∴△BCG≌△CAF(ASA),
∴CF=BG;
(2)∵PC∥AG,
∴∠PCA=∠CAG,
∵AC=BC,∠ACG=∠BCG,CG=CG,
∴△ACG≌△BCG,
∴∠CAG=∠CBE,
∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,
∠PGC=∠GCB+∠CBE=∠CBE+45°,
∴∠PCG=∠PGC,
∴PC=PG,
∵PB=BG+PG,BG=CF,
∴PB=CF+CP;
过E作EM⊥AG,交AG于M,
∵S△AEG=![]() AGEM=3
AGEM=3![]() ,
,
由(2)得:△ACG≌△BCG,
∴BG=AG=6,
∴![]() ×6×EM=3
×6×EM=3![]() ,
,
EM=![]() ,
,
设∠FCH=x°,则∠GAC=2x°,
∴∠ACF=∠EBC=∠GAC=2x°,
∵∠ACH=45°,
∴2x+x=45,
x=15,
∴∠ACF=∠GAC=30°,
在Rt△AEM中,AE=2EM=2![]() ,
,
![]()
∴M是AG的中点,
∴AE=EG=2![]() ,
,
∴BE=BG+EG=6+2![]() ,
,
在Rt△ECB中,∠EBC=30°,
∴CE=![]() BE=3+
BE=3+![]() ,
,
∴AC=AE+EC=2![]() +3+
+3+![]() =3
=3![]() +3.
+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家蔬菜公司收购到某种绿色蔬菜200吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式
粗加工后销售
精加工后销售
每吨获利(元)
500
800
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求20天刚好加工完200吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过16天的时间内,将200吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
-
科目: 来源: 题型:
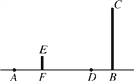
查看答案和解析>>【题目】如图,在一座大厦(图中BC所示)前面30m的地面上,有一盏地灯A照射大厦,身高为1.6m的小亮(图中EF所示)站在大厦和灯之间,若小亮从现在所处位置径直走向大厦,当他走到距离大厦只有5m的D处时停下.
(1)请在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC上的影子;
(2)请你求出此时小亮的影长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从相距480km的A.B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
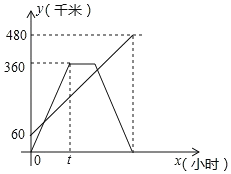
(1)乙车的速度是___千米/时,t=___小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出两车相距150千米时x的取值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
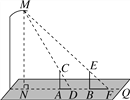
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值
 ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.
A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等式
 在实数范围内成立,其中a、x、y是两两不同的实数,则
在实数范围内成立,其中a、x、y是两两不同的实数,则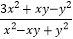 的值是( )
的值是( )A. 3 B.
 C. 2 D.
C. 2 D. 
相关试题

