搜索
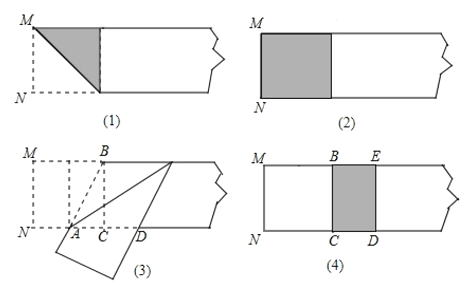
【题目】我们做个折纸游戏：第一步：在一张矩形纸片的一端，利用图
的方法折出一个正方形，然后把纸片展开；第二步：如图
，把这个正方形折成两个相等的矩形，再把纸片展开；第三步：折出内侧矩形的对角线
，并把它折到图
中所示的
处；第四步：如图
， 展平纸片，按照所得的
点折出
．则矩形
的宽
与长
的比是__________．
参考答案：
【答案】
【解析】
设正方形的边长为2a，由折叠的性质，可得AC＝正方形的边长×
＝a，在Rt△ABC中，利用勾股定理可求出AB与正方形的边长之间的关系，再求出CD＝
aa，即可求解．
在正方形BCNM中，令NC＝2a，∴BC=NC=2a，
∵A为NC的中点，
∴AC＝NC＝a．
在Rt△ABC中，AB＝
=a．
又∵AD＝AB，
∴CD＝ADAC＝（1）a．
∴矩形BCDE的宽CD与长BC的比＝
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【知识链接】 有理化因式：两个含有根式的非零代数式相乘，如果它们的积不含有根式，那么这两个代数式相互叫做有理化因式．
例如：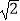
的有理化因式是 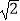；1﹣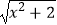 
的有理化因式是1+ ．
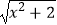分母有理化：分母有理化又称“有理化分母”，也就是把分母中的根号化去．指的是如果代数式中分母有根号，那么通常将分子、分母同乘以分母的有理化因式，达到化去分母中根号的目的．如：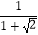
= 
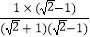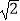= ﹣1，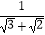 
= 
= 
﹣ ．
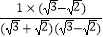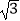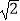（1）【知识理解】 填空：2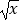
的有理化因式是；
直接写出下列各式分母有理化的结果：
①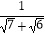
=；②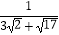 
= ．
（2）【启发运用】 计算： + +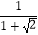 
+…+ 
． -
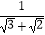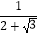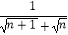科目： 来源： 题型：
查看答案和解析>>【题目】完成下列证明：如图，已知AD⊥BC，EF⊥BC，∠1=∠2．
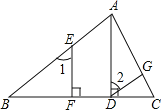
求证：DG∥BA．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠EFB=90°，∠ADB=90°（______）
∴∠EFB=∠ADB（等量代换）
∴EF∥AD（______）
∴∠1=∠BAD（______）
又∵∠1=∠2（已知）
∴∠______=∠______（等量代换）
∴DG∥BA．（______）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解题： 学习了二次根式后，你会发现一些含有根号的式子可以写成另一个式子的平方，如3+2
=（1+ ）2 ， 我们来进行以下的探索：
设a+b =（m+n ）2（其中a，b，m，n都是正整数），则有a+b =m2+2n2+2mn ，∴a=m+2n2 ， b=2mn
， 这样就得出了把类似a+b 的式子化为平方式的方法．
请仿照上述方法探索并解决下列问题：
（1）当a，b，m，n都为正整数时，若a﹣b
=（m﹣n ）2 ， 用含m，n的式子分别表示a，b，得a= ， b=；
（2）利用上述方法，找一组正整数a，b，m，n填空：﹣ =（﹣ ）2
（3）a﹣4 =（m﹣n ）2且a，m，n都为正整数，求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（ ）
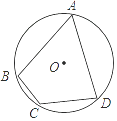
A.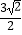
B.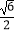
C.
D.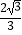
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD为⊙O的内接四边形．延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC=50°，则∠DBC的度数为（ ）
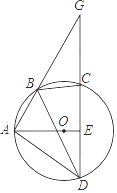
A.50°
B.60°
C.80°
D.90° -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．
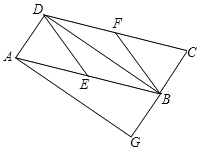
（1）求证：△ADE≌△CBF；
（2）若四边形 BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．
相关试题
