【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
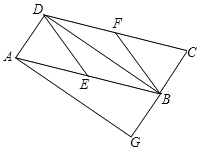
(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
参考答案:
【答案】(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD.
CD.
∴AE=CF.
∴△ADE≌△CBF(SAS).
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.

【解析】试题分析:本题主要考查了平行四边形的基本性质和矩形的判定及全等三角形的判定.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.三角形全等的判定条件:SSS,SAS,AAS,ASA.
(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等; (2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD.
CD.
∴AE=CF.
在△AED和△CBF中,
 ,
,
∴△ADE≌△CBF(SAS).
(2)当四边形BEDF是菱形时,四边形AGBD是矩形.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们做个折纸游戏:第一步:在一张矩形纸片的一端,利用图
 的方法折出一个正方形,然后把纸片展开;第二步:如图
的方法折出一个正方形,然后把纸片展开;第二步:如图 ,把这个正方形折成两个相等的矩形,再把纸片展开;第三步:折出内侧矩形的对角线
,把这个正方形折成两个相等的矩形,再把纸片展开;第三步:折出内侧矩形的对角线 ,并把它折到图
,并把它折到图 中所示的
中所示的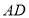 处;第四步:如图
处;第四步:如图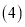 , 展平纸片,按照所得的
, 展平纸片,按照所得的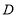 点折出
点折出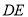 .则矩形
.则矩形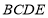 的宽
的宽 与长
与长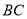 的比是__________.
的比是__________.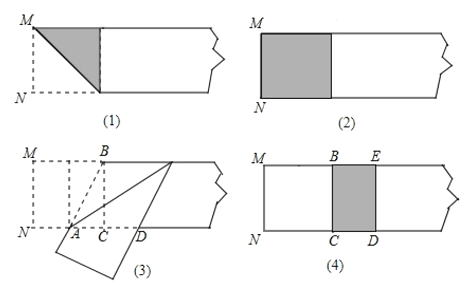
-
科目: 来源: 题型:
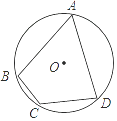
查看答案和解析>>【题目】如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
A.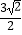
B.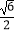
C.
D.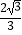
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
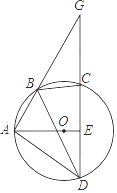
A.50°
B.60°
C.80°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(立方米)之间关系的图象如图所示,根据图象回答:
(1)该市自来水收费,每户用水不超过5立方米时,每立方米收费多少元?超过5立方米时,超过的部分每立方米收费多少元?
(2)求出y与x之间的关系式.
(3)若某户居民某月用水量为3.5立方米,则应交水费多少元?若某户居民某月交水费17元,则该户居民用水多少立方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形纸片
 沿对角线
沿对角线 翻折,使点
翻折,使点 落在平行四边形
落在平行四边形 所在平面内,
所在平面内, 和
和 相交于点
相交于点 ,连接
,连接
 判断
判断 和
和 的位置关系,并证明.
的位置关系,并证明. 在图1中,若
在图1中,若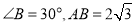 ,是否存在
,是否存在 恰好为直角三角形的情形?若存在,求出
恰好为直角三角形的情形?若存在,求出 的长度:若不存在,请说明理由.
的长度:若不存在,请说明理由. 若将图中平行四边形纸片
若将图中平行四边形纸片 换成矩形纸片
换成矩形纸片 ,沿对角线折叠发现所得图形是轴对称图形;将所得图形沿其对称轴再次折叠后,得到的仍是轴对称图形.则矩形纸片
,沿对角线折叠发现所得图形是轴对称图形;将所得图形沿其对称轴再次折叠后,得到的仍是轴对称图形.则矩形纸片 的长宽之比是多少?请直接写出结果.
的长宽之比是多少?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,
 =
=  ,过点C作CE⊥AD,垂足为E,若AE=3,DE=
,过点C作CE⊥AD,垂足为E,若AE=3,DE=  ,求∠ABC的度数.
,求∠ABC的度数.
相关试题

