【题目】如图,已知![]() 中直径
中直径![]() ,半径
,半径![]() ,点
,点![]() 是半圆
是半圆![]() 的三等分点,点
的三等分点,点![]() 是半径
是半径![]() 上的动点,使
上的动点,使![]() 的值最小时,
的值最小时,![]() ( )
( )

A.1B.![]() C.2D.3
C.2D.3
参考答案:
【答案】C
【解析】
接PA.因为OC⊥直径AB,所以CO垂直平分AB.根据“垂直平分线上的点到线段两端的距离相等”得PB+PD=PA+PD,根据“两点之间线段最短”可知,连接BD,与CO相交于P,则AD的长度即为PB+PD的最小值.然后利用解直角三角形的知识求出PO的值即可.
连接PA,与CO相交于P,连接BD.
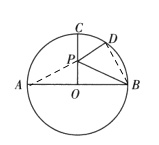
∵OC⊥AB,
∴CO垂直平分AB,
∴PA=PB,
∴PB+PD=PA+PD,
∴根据“两点之间线段最短”可知,AD的长度即为PB+PD的最小值.
∵AB为直径,
∴∠D=90°,
∵点![]() 是半圆
是半圆![]() 的三等分点,
的三等分点,
∴ ![]() 的度数为60°,
的度数为60°,
∴∠A=30°,
∴![]() ,
,
∴![]() ;
;
故答案为:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电影《我和我的祖国》上映以来好评如潮,某影评平台随机调查了部分观众对这部电影的评分(满分10分),并将调查结果制成了如下不完整的统计图表(表中每组数据不包括最小值,包括最大值):
等级
频数
频率
A等(9.6分~10分)
a
0.7
B等(8.8分~9.6分)
3
0.15
C等(8.2分~8.8分)
b
c
D等(8.2分及以下)
1
0.05
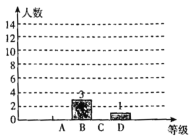
请根据图表信息,解答下列问题:
(1)这次共随机调查了_______名观众,a=______;b=______;c=______;
(2)补全条形统计图;
(3)若某电影院同时上映《我和我的祖国》、《中国机长》和《烈火英雄》,红红和兰兰分别选择其中一部电影观看,求她们选中同一部电影的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线C1的顶点在抛物线C2上,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2为“互相关联”的抛物线.如图,已知抛物线
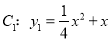 与
与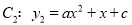 是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).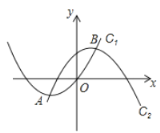
(1)直接写出点A,B的坐标和抛物线C2的解析式.
(2)抛物线C2上是否存在点E,使得△ABE是以AB为直角边的直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ABC=2∠ACB,BD平分∠ABC交AC于点D.
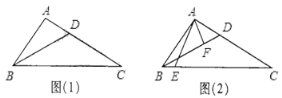
(1)如图(1),若AB=3,AC=5,求AD的长;
(2)如图(2),过点A分别作AC,BD的垂线,分别交BC,BD于点E,F.
①求证:∠ABC=∠EAF;
②求
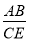 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=
 ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
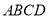 中,
中,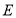 为
为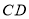 的中点,
的中点,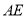 的垂直平分线分别交
的垂直平分线分别交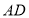 ,
,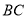 及
及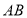 的延长线于点
的延长线于点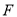 ,
, ,
,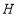 ,连接
,连接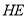 ,
,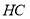 ,
,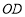 ,连接
,连接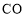 并延长交
并延长交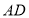 于点
于点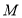 .则下列结论中:①
.则下列结论中:①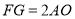 ;②
;②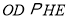 ;③
;③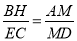 ;④
;④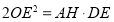 ;⑤
;⑤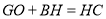 .正确结论的个数有( )
.正确结论的个数有( )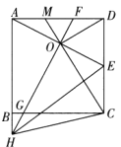
A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】草莓是种老少皆宜的食品,深受市民欢迎.今年3月份,甲,乙两超市分别用3000元以相同的进价购进质量相同的草莓.甲超市销售方案是:将草莓按大小分类包装销售,其中大草莓400千克,以进价的2倍价格销售,剩下的小草莓以高于进价的10%销售.乙超市销售方案是:不将草莓按大小分类,直接包装销售,价格按甲超市大、小两种草莓售价的平均数定价.若两超市将草莓全部售完,其中甲超市获利2100元(其他成本不计).
(1)草莓进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
相关试题

