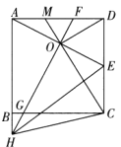
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 及
及![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .则下列结论中:①
.则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确结论的个数有( )
.正确结论的个数有( )
A.2B.3C.4D.5
参考答案:
【答案】B
【解析】
①作辅助线,构建三角形全等,证明△ADE≌△GKF,则FG=AE,可得FG=2AO;
②证明∠HEA=∠AED=∠ODE,OE≠DE,则∠DOE≠∠HEA,OD与HE不平行;
③设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,证明△ADE∽△HOA,得![]() ,所以
,所以![]() ,根据AR∥CD,得
,根据AR∥CD,得![]() ,则
,则![]() ;④证明△HAE∽△ODE,可得
;④证明△HAE∽△ODE,可得![]() ,等量代换可得OE2=AHDE;
,等量代换可得OE2=AHDE;
⑤分别计算HC、OG、BH的长,可得结论.
:①如图,过G作GK⊥AD于K,
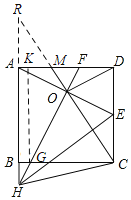
∴∠GKF=90°,
∵四边形ABCD是正方形,
∴∠ADE=90°,AD=AB=GK,
∴∠ADE=∠GKF,
∵AE⊥FH,
∴∠AOF=∠OAF+∠AFO=90°,
∵∠OAF+∠AED=90°,
∴∠AFO=∠AED,
∴△ADE≌△GKF,
∴FG=AE,
∵FH是AE的中垂线,
∴AE=2AO,
∴FG=2AO,
故①正确;
②∵FH是AE的中垂线,
∴AH=EH,
∴∠HAE=∠HEA,
∵AB∥CD,
∴∠HAE=∠AED,
Rt△ADE中,∵O是AE的中点,
∴![]() ,
,
∴∠ODE=∠AED,
∴∠HEA=∠AED=∠ODE,
当∠DOE=∠HEA时,OD∥HE,
但AE>AD,即AE>CD,
∴OE>DE,即∠DOE≠∠HEA,
∴OD与HE不平行,
故②不正确;
③设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,
∴![]() ,
,![]() ,
,
易得△ADE∽△HOA,
∴![]() ,
,
∴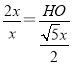 ,
,
∴![]() ,
,
Rt△AHO中,由勾股定理得:![]() ,
,
∴BH=AH-AB= ![]() ,
,
∴![]() ,
,
延长CM、BA交于R,
∵RA∥CE,
∴∠ARO=∠ECO,
∵AO=EO,∠ROA=∠COE,
∴△ARO≌△ECO,
∴AR=CE,
∵AR∥CD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故③正确;
④由①知:∠HAE=∠AEH=∠OED=∠ODE,
∴△HAE∽△ODE,
∴![]() ,
,
∵AE=2OE,OD=OE,
∴OE2OE=AHDE,
∴2OE2=AHDE,
故④正确;
⑤由③知:![]() ,
,
∵![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴OG+BH≠HC,
故⑤不正确;
本题正确的有;①③④,3个,
故答案为:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ABC=2∠ACB,BD平分∠ABC交AC于点D.
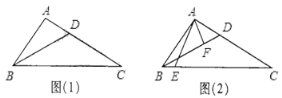
(1)如图(1),若AB=3,AC=5,求AD的长;
(2)如图(2),过点A分别作AC,BD的垂线,分别交BC,BD于点E,F.
①求证:∠ABC=∠EAF;
②求
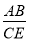 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
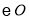 中直径
中直径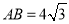 ,半径
,半径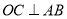 ,点
,点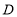 是半圆
是半圆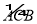 的三等分点,点
的三等分点,点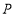 是半径
是半径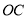 上的动点,使
上的动点,使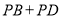 的值最小时,
的值最小时, ( )
( )
A.1B.
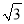 C.2D.3
C.2D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=
 ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】草莓是种老少皆宜的食品,深受市民欢迎.今年3月份,甲,乙两超市分别用3000元以相同的进价购进质量相同的草莓.甲超市销售方案是:将草莓按大小分类包装销售,其中大草莓400千克,以进价的2倍价格销售,剩下的小草莓以高于进价的10%销售.乙超市销售方案是:不将草莓按大小分类,直接包装销售,价格按甲超市大、小两种草莓售价的平均数定价.若两超市将草莓全部售完,其中甲超市获利2100元(其他成本不计).
(1)草莓进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在课外研究中,设计如下题目:直线
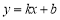 过点
过点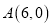 ,
,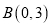 ,直线
,直线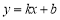 与曲线
与曲线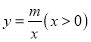 交于点
交于点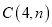 .
.(1)求直线和曲线的关系式.(图1)
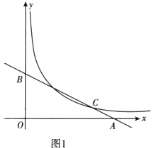
(2)小明发现曲线
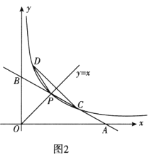
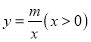 关于直线
关于直线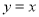 对称,他把曲线
对称,他把曲线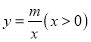 与直线
与直线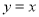 的交点
的交点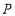 叫做曲线的顶点.(图2)
叫做曲线的顶点.(图2)①直接写出
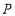 点的坐标;
点的坐标;②若点
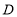 从
从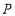 点出发向上运动,运动到
点出发向上运动,运动到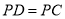 时停止,求此时
时停止,求此时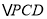 的面积.
的面积.
相关试题

