【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=![]() ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.

A. 5 B. 4 C. 3 D. 2
参考答案:
【答案】C
【解析】
根据二次函数图象与系数的关系,二次函数与x轴交于点A(-1,0)、B(3,0),可知二次函数的对称轴为x=![]() =1,即-
=1,即-![]() =1,可得2a与b的关系;将A、B两点代入可得c、b的关系;函数开口向下,x=1时取得最小值,则m≠1,可判断③;根据图象AD=BD,顶点坐标,判断④;由图象知BC≠AC,从而可以判断⑤.
=1,可得2a与b的关系;将A、B两点代入可得c、b的关系;函数开口向下,x=1时取得最小值,则m≠1,可判断③;根据图象AD=BD,顶点坐标,判断④;由图象知BC≠AC,从而可以判断⑤.
解:①∵二次函数与x轴交于点A(-1,0)、B(3,0).
∴二次函数的对称轴为x=![]() =1,即-
=1,即-![]() =1,
=1,
∴2a+b=0.
故①正确;
②∵二次函数y=ax2+bx+c与x轴交于点A(-1,0)、B(3,0).
∴a-b+c=0,9a+3b+c=0.
又∵b=-2a.
∴3b=-6a,a-(-2a)+c=0.
∴3b=-6a,2c=-6a.
∴2c=3b.
故②错误;
③∵抛物线开口向上,对称轴是x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.
故③正确;
④∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1-(-1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,-2).
∵二次函数的顶点D为(1,-2),过点A(-1,0).
设二次函数解析式为y=a(x-1)2-2.
∴0=a(-1-1)2-2.
解得a=![]() .
.
故④正确;
⑤由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.
故⑤错误.
故①③④正确,②⑤错误.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
 MF.其中正确结论的是( )
MF.其中正确结论的是( )
A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )

A. π B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:学习了分式运算后,老师布置了这样一道计算题:
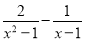 ,甲、乙两位同学的解答过程分别如下:
,甲、乙两位同学的解答过程分别如下:甲同学:
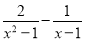
 ①
① ②
② ③
③ ④
④乙同学:
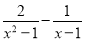
 ①
① ②
② ③
③ ④
④老师发现这两位同学的解答过程都有错误.
请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正.
(1)我选择________同学的解答过程进行分析. (填“甲”或“乙”)
(2)该同学的解答从第________步开始出现错误(填序号),错误的原因是________;
(3)请写出正确解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
我区在一项工程招标时,接到甲、乙两个工程队的投标书,从投标书中得知:每施工一天,甲工程队要
 万元,乙工程队要
万元,乙工程队要 万元,工程小组根据甲、乙两队标书的测算,有三种方案:
万元,工程小组根据甲、乙两队标书的测算,有三种方案: 甲队单独完成这个工程,刚好如期完成;
甲队单独完成这个工程,刚好如期完成; 乙队单独完成这个工程要比规定时间多用5天;
乙队单独完成这个工程要比规定时间多用5天; **********,剩下的工程由乙队单独做,也正好如期完成. 方案
**********,剩下的工程由乙队单独做,也正好如期完成. 方案 中“星号”部分被损毁了. 已知,一个同学设规定的工期为
中“星号”部分被损毁了. 已知,一个同学设规定的工期为 天,根据题意列出方程:
天,根据题意列出方程:
(1)请将方案中“星号”部分补充出来________________;
(2)你认为哪个方案节省工程款,请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在四边形
 中,
中, ,点
,点 是
是 的中点,若
的中点,若 是
是 的平分线,试判断
的平分线,试判断 ,
, ,
, 之间的等量关系.
之间的等量关系.解决此问题可以用如下方法:延长
 交
交 的延长线于点
的延长线于点 ,易证
,易证 得到
得到 ,从而把
,从而把 ,
, ,
, 转化在一个三角形中即可判断.
转化在一个三角形中即可判断. ,
, ,
, 之间的等量关系________;
之间的等量关系________;(2)问题探究:如图②,在四边形
 中,
中, ,
, 与
与 的延长线交于点
的延长线交于点 ,点
,点 是
是 的中点,若
的中点,若 是
是 的平分线,试探究
的平分线,试探究 ,
, ,
, 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=130°,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F,则∠MAN为( )

A.80°B.70°C.60°D.50°
相关试题

