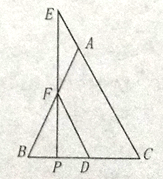
【题目】如图,在ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.求证:△AEF是等腰三角形.
参考答案:
【答案】见解析
【解析】试题分析:
由已知条件易证△BDF是等腰三角形,结合FP⊥BD可得∠DFP=∠BFP=∠AFE;再由DF∥AC可得∠E=∠DFP,从而可得∠AFE=∠E,即可得到AE=AF.
试题解析:
∵FD∥AC,
∴∠PFD=∠E,∠FDB=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B,
∴FB=FD.
又∵EP⊥BC,
∴∠PFB=∠PFD,
∵∠PFB=∠AFE,
∴∠PFD=∠AFE,
又∵∠PFD=∠E,
∴∠E=∠AFE,
∴AE=AF,即△AEF是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆的半径扩大到原来的3倍,周长扩大到原来的____倍.面积扩大到原来的_______倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:
①m=3;
②当∠APB=120°时,a= ;
;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥
正确的是( )
A.①②
B.③④
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BF,∠1与∠2互补.
(1)试说明:FG∥AB;
(2)若∠CFG=60°,∠2=150°,则DE与AC垂直吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的一边长为5,另两边长分别是二次函数y=x2﹣6x+m与x轴的交点坐标的横坐标的值,则m的取值范围为
-
科目: 来源: 题型:
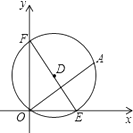
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A,O,分别与两坐标轴的正半轴交于点E,F.当EF⊥OA时,此时EF= .
相关试题

