【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
参考答案:
【答案】(1) 2小时;(2)8.75千米;(3)2.5小时或3.5小时或5.75小时两队间间隔的路程为1千米
【解析】分析:(1)设乙队追上甲队需要x小时,根据乙队比甲队快的速度×时间=甲队比乙队先走的路程可列出方程,解出即可得出时间;
(2)先计算出联络员所走的时间,再由路程=速度×时间即可得出联络员走的路程.
(3)要分3种情况讨论:①当甲队出发1小时后,相遇前与乙队相距1千米;②当甲队出发1小时后,相遇后与乙队相距1千米;③乙队到达后两队间间隔的路程为1千米;分别列出方程求解即可.
详解:(1)设乙队追上甲队需要x小时,
根据题意得:![]()
解得:![]()
答:乙队追上甲队需要2小时.
(2)4×1÷(6+10)=0.25(小时),
[(1+0.25)×4﹣0.25×10]÷(10﹣6)
=2.5÷4
=0.625(小时),
(0.25+0.625)×10=8.75(千米).
答:他跑步的总路程是8.75千米.
(3)要分三种情况讨论:
设t小时两队间间隔的路程为1千米,则
①当甲队出发1小时后,相遇前与乙队相距1千米,
由题意得![]()
解得:![]()
②当甲队出发1小时后,相遇后与乙队相距1千米,
由题意得:![]()
解得:![]()
③乙队到达后两队间间隔的路程为1千米,
由题意得:![]()
解得:![]()
答:2.5小时或3.5小时或5.75小时两队间间隔的路程为1千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:像
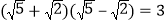 、
、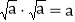
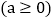 、
、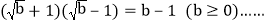 两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式
两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式 例如,
例如,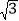 与
与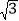 、
、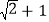 与
与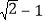 、
、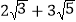 与
与 等都是互为有理化因式
等都是互为有理化因式 在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.例如;
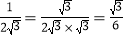 ;
;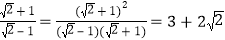 .
.解答下列问题:
(1)
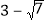 与________互为有理化因式,将
与________互为有理化因式,将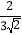 分母有理化得________;
分母有理化得________;(2)计算:
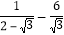 ;
;(3)己知有理数a、b满足
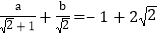 ,求a、b的值.
,求a、b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,∠AOB=∠COD=90°,OM平分∠AOC,ON平分∠BOD.
(1)已知∠BOC=20°,且∠AOD小于平角,求∠MON的度数;
(2)若(1)中∠BOC=α,其它条件不变,求∠MON的度数;
(3)如图②,若∠BOC=α,且∠AOD大于平角,其它条件不变,求∠MON的度数.
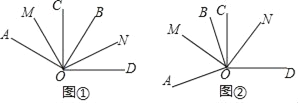
-
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线的解析式为y=ax2 , 过点B1(1,0)作x轴的垂线,交抛物线于点A1(1,2);过点B2(
 ,0)作x轴的垂线,交抛物线于点A2;…;过点Bn((
,0)作x轴的垂线,交抛物线于点A2;…;过点Bn((  )n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
)n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
(1)求a的值;
(2)直接写出线段AnBn , BnBn+1的长(用含n的式子表示);
(3)在系列Rt△AnBnBn+1中,探究下列问题:
①当n为何值时,Rt△AnBnBn+1是等腰直角三角形?
②设1≤k<m≤n(k,m均为正整数),问:是否存在Rt△AkBkBk+1与Rt△AmBmBm+1相似?若存在,求出其相似比;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2019次输出的结果为( )

A. 3 B. 6 C. 12 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
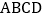 中,对角线
中,对角线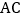 、
、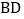 相交于点
相交于点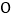 ,下列条件不能判定这个四边形是平行四边形的是( )
,下列条件不能判定这个四边形是平行四边形的是( )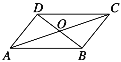
A. AB∥DC,AD∥BC B. AO=CO,BO=DO
C. AB∥DC,AD=BC D. AB=DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·
 )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

相关试题

