【题目】如图,在平行四边形![]() 中,
中,![]() 于
于![]() 为
为![]() 的中点,则
的中点,则![]() 的大小是( )
的大小是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
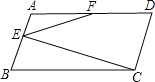
过F作AB的平行线FG,由于F是AD的中点,那么G是BC的中点,即Rt△BCE斜边上的中点,由此可得BC=2EG=2FG,即△GEF、△BEG都是等腰三角形,因此求∠B的度数,只需求得∠BEG的度数即可;易知四边形ABGF是平行四边形,得∠EFG=∠AEF,由此可求得∠FEG的度数,即可得到∠AEG的度数,根据邻补角的定义可得∠BEG的度数,由此得解.
解:过F作FG∥AB交BC于G,连接EG,
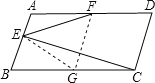
∵在平行四边形ABCD中,AB∥CD,AD∥BC,
∴FG∥AB∥CD,
∵FG∥AB,AD∥BC,
∴四边形ABGF是平行四边形,
∴AF=BG,
又∵F为AD中点
∴G是BC的中点;
∵BC=2AB,F为AD的中点,
∴BG=AB=FG=AF,
∵在Rt△BEC中,EG是斜边上的中线,
∴BG=GE=FG=![]() BC;
BC;
∴∠BEG=∠B=72°,
∴∠AEG=∠AEF+∠FEG=180°﹣∠BEG=108°,
∵AE∥FG,
∴∠EFG=∠AEF,
∵GE=FG,
∴∠EFG=∠FEG,
∴∠AEF=∠FEG=![]() ∠AEG=54°,
∠AEG=54°,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个正方形的边长都为1的正方形网格中,点
 都在格点上,从这四个点中任取三个点构成三角形,则构成的三角形中,不是直角三角形的是( )
都在格点上,从这四个点中任取三个点构成三角形,则构成的三角形中,不是直角三角形的是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
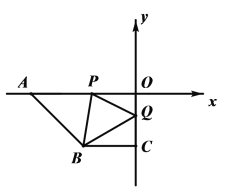
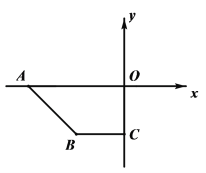
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足
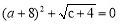 ,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.(1)直接写出点B的坐标,AO和BC位置关系是;
(2)当P、Q分别是线段AO,OC上时,连接PB,QB,使
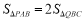 ,求出点P的坐标;
,求出点P的坐标;(3)在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 和
和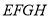 都是正方形,点
都是正方形,点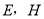 在
在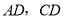 边上,点
边上,点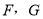 在对角线
在对角线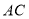 上,若
上,若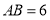 ,则
,则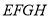 的面积是( )
的面积是( )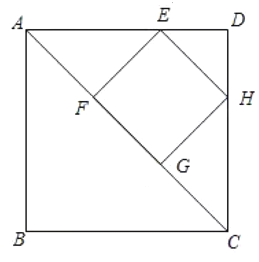
A.6B.8C.9D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+k(k≠0)与双曲线
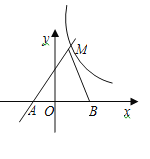
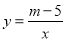 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A.(1)求m的取值范围和点A的坐标;
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某工艺厂为迎“五一”,设计了一款成本为20元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
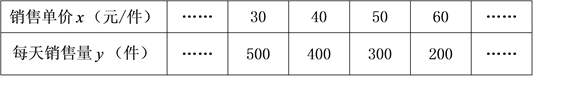
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.
(1)如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.
(2)一年中进入该公园超过多少次时,A类年票比较合算?
相关试题

