【题目】我市某工艺厂为迎“五一”,设计了一款成本为20元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
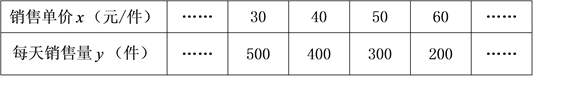
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
参考答案:
【答案】(1)y与x的函数关系是一次函数的关系,函数关系式为y=-10x+800 (20<x<80);(2)当销售单价定为50元时,每天获得的利润最大,最大利润是9000 元;(3当销售单价定为45元时,每天获得的利润最大.
【解析】试题分析:(1)描点,由图可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)利润=销售总价-成本总价=单件利润×销售量.据此得表达式,运用性质求最值;
(3)根据自变量的取值范围结合函数图象解答.
试题解析:(1)画图如图,
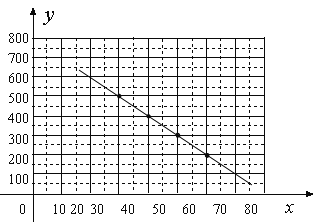
由图可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0)
∵这个一次函数的图象经过(30,500)
(40,400)这两点,
∴![]() ,
,
解得![]()
∴函数关系式是:y=-10x+800(20≤x≤80)
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得
W=(x-20)(-10x+800)
=-10x2+1000x-16000
=-10(x-50)2+9000,(20≤x≤80)
∴当x=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元.
(3)对于函数W=-10(x-50)2+9000,当x≤45时,
W的值随着x值的增大而增大,
∴销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 和
和 都是正方形,点
都是正方形,点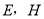 在
在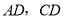 边上,点
边上,点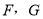 在对角线
在对角线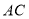 上,若
上,若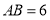 ,则
,则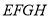 的面积是( )
的面积是( )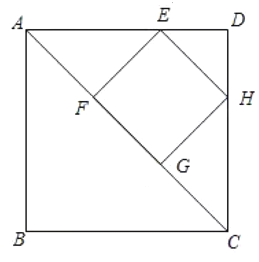
A.6B.8C.9D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
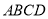 中,
中,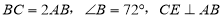 于
于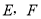 为
为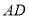 的中点,则
的中点,则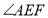 的大小是( )
的大小是( )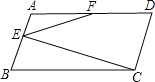
A.
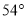 B.
B.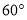 C.
C.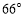 D.
D.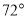
-
科目: 来源: 题型:
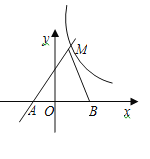
查看答案和解析>>【题目】如图,直线y=kx+k(k≠0)与双曲线
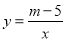 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A.(1)求m的取值范围和点A的坐标;
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.
(1)如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.
(2)一年中进入该公园超过多少次时,A类年票比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,E是等腰Rt△ABC边AC上的一个动点(点E与A、C不重合),以CE为一边在Rt△ABC作等腰Rt△CDE,连结AD,BE.我们探究下列图中线段AD,、线段BE 的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的等腰Rt△CDE绕着点C按顺时针方向旋转任意角度
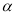 ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中等腰直角三角形改为直角三角形(如图4—6),且AC=a,BC=b,CD=ka,CE=kb (a
 b,k
b,k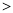 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.(3)在第(2)题图5中,连结BD、AE,且a=4,b=3,k=
 ,求BD2+AE2的值.
,求BD2+AE2的值.
-
科目: 来源: 题型:
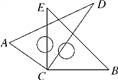
查看答案和解析>>【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的关系,并说明理由.
相关试题

