搜索
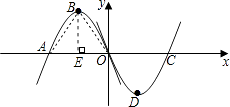
【题目】如图所示，抛物线y=ax2+bx（a＜0）的图象与x轴交于A、O两点，顶点为B，将该抛物线的图象绕原点O旋转180°后，与x轴交于点C，顶点为D，若此时四边形ABCD恰好为矩形，则b的值为 ． 
参考答案：
【答案】﹣2 
【解析】解：如图，连接AB、OB．过点B作BE⊥x轴于点E． 要使平行四边形ABCD是矩形，必须满足AC=BD，
∴OA=OB．
∵点B是抛物线的顶点，
∴AB=OB，
∴△ABO是等边三角形，
∠BAE=60°，AE= 
OA．
∵y=ax2+bx=ax（x+ 
）=0，y=ax2+bx=a（x+ 
）2﹣ 
∴A（﹣ ，0），B（﹣ ，﹣ ），
∴tan60°= 
= 
= ．
解得 b=﹣2 ．
故答案是：﹣2 ．
【考点精析】认真审题，首先需要了解二次函数图象的平移(平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察以下等式：
第1个等式：
+
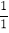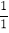+×=1，第2个等式：
+
+×=1，第3个等式：
+
+×=1，第4个等式：
+
+×=1，第5个等式：
+
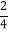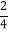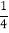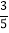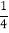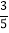+×=1，……
按照以上规律，解决下列问题：
（1）写出第6个等式：_____；
（2）写出你猜想的第n个等式：_____（用含n的等式表示），并证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若我们规定三角“
”表示为：abc；方框“
”表示为：（xm+yn）．例如：
=1×19×3÷（24+31）=3．请根据这个规定解答下列问题：（1）计算：
= ______ ；（2）代数式
为完全平方式，则k= ______ ；（3）解方程：
=6x2+7． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=
，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2 ． 上述说法正确的是（ ）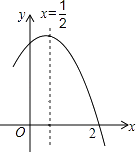 
A.①②④
B.③④
C.①③④
D.①② -
科目： 来源： 题型：
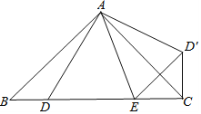
查看答案和解析>>【题目】如图，已知△ABC中，∠BAC=90°，AB=AC，D、E是BC边上的点，将△ABD绕点A旋转，得到△ACD′．
（1）当∠DAE=45°时，求证：DE=D′E；
（2）在（1）得条件下，猜想：BD2、DE2、CE2有怎样的数量关系？请写出，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．
我们有多少种剪法，图1是其中的一种方法：定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
请你在图2中用三种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程x2+（m+3）x+m+1=0．
（1）求证：无论m取何值，原方程总有两个不相等的实数根：
（2）若x1 ， x2是原方程的两根，且|x1﹣x2|=2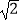
，求m的值，并求出此时方程的两根．
相关试题
