搜索
【题目】已知直线
经过点
，且与
交于点
，在
轴上存在一点
使得
的值最小，则点的坐标为_______．
参考答案：
【答案】
【解析】
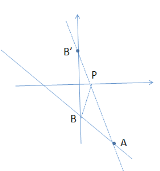
先作点B关于x轴对称的点B'，连接AB'，交x轴于P，则点P即为所求，根据待定系数法求得直线为y=-x-2，进而得到点B的坐标以及点B'的坐标，再根据待定系数法求得直线AB'的解析式，即可得到点P的坐标．
如图所示，作点B关于x轴对称的点B'，连接AB'，交x轴于P，则点P即为所求，
把A(2,-4）代入y=-x+b可得，b=-2，
∴直线为y=-x-2，
令x=0，则y=-2，即B(0,-2)
∴B'(0,2）
设直线AB'的解析式为y=kx+n，
把A(2,-4)，B'(0,2）代入可得，
解得
∴直线AB'的解析式为y=-3x+2，
令y=0，则x=
∴P(,0）
故答案为：(,0)
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：
①抛物线过原点；
②4a+b+c=0；
③a﹣b+c＜0；
④抛物线的顶点坐标为（2，b）；
⑤当x＜2时，y随x增大而增大．
其中结论正确的是（ ）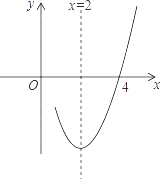
A.①②③
B.③④⑤
C.①②④
D.①④⑤ -
科目： 来源： 题型：
查看答案和解析>>【题目】若x1 ， x2（x1＜x2）是方程（x﹣a）（x﹣b）=﹣1（a＜b）的两根，则实数x1 ， x2 ， a，b的大小关系是（ ）
A.a＜x1＜x2＜b
B.x1＜a＜x2＜b
C.x1＜a＜b＜x2
D.x1＜x2＜a＜b -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，BD⊥AC于点D．
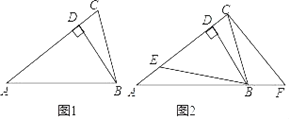
（1）若∠C＝∠ABC＝2∠A，则∠DBC＝ °；
（2）若∠A＝2∠CBD，求证：∠ACB＝∠ABC；
（3）如图2，在（2）的条件下，E是AD上一点，F是AB延长线上一点，连接BE、CF，使∠BEC＝∠CFB，∠BCF＝2∠ABE，求∠EBC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校学生会向全校
名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答下列问题：（1）本次接受随机抽样调查的学生人数为 人，图
中
的值是 ．（2）补全图2的统计图．
（3）求本次调查获取的样本数据的平均数、众数和中位数；
（4）根据样本数据，估计该校本次活动捐款金额为
元的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的二次函数y=ax2+（a2﹣1）x﹣a的图象与x轴的一个交点的坐标为（m，0）．若2＜m＜3，则a的取值范围是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧，其图象与x轴交于点A（﹣1，0）与点C（x2 ， 0），且与y轴交于点B（0，﹣2），小强得到以下结论：①0＜a＜2；②﹣1＜b＜0；③c=﹣1；④当|a|=|b|时x2＞
﹣1；以上结论中正确结论的序号为 ． 
相关试题
