【题目】如图1,在△ABC中,BD⊥AC于点D.
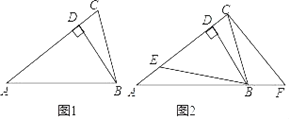
(1)若∠C=∠ABC=2∠A,则∠DBC= °;
(2)若∠A=2∠CBD,求证:∠ACB=∠ABC;
(3)如图2,在(2)的条件下,E是AD上一点,F是AB延长线上一点,连接BE、CF,使∠BEC=∠CFB,∠BCF=2∠ABE,求∠EBC的度数.
参考答案:
【答案】(1)18;(2)见解析;(3)∠EBC=60°.
【解析】
(1)由于∠C=∠ABC=2∠A=2α,所以利用三角形内角和定理即可求出α的值,从而可求出∠DBC的值;
(2)由BD⊥AC,所以∠BDC=∠ADB=90°,所以∠DCB+∠DBC=90°,∠A+∠ABD=90°,所以∠ACB=90°﹣∠DBC,∠ABD=90°﹣∠A,所以∠ABD=90°﹣2∠DBC,又易证∠ABC=∠ABD+∠DBC=90°﹣∠DBC,所以∠ACB=∠ABC;
(3)由于∠ABC=∠F+∠BCF,∠ABC=∠ABE+∠EBC,∠BCF=2∠ABE,所以∠EBC=∠F+∠ABE,易证∠ACB=2∠ABE+∠F,∠F+∠ABE+2∠ABE+∠F+∠F=180°,从而可求出∠F+∠ABE=60°,即∠EBC=60°
解:(1)∵设∠A=α
∴∠C=∠ABC=2α,
∴α+2α+2α=180°,
∴α=36°,
∴∠C=2α=72°,
∴∠DBC=90°﹣∠C=18°
(2)∵BD⊥AC,
∴∠BDC=∠ADB=90°,
∴∠DCB+∠DBC=90°
∠A+∠ABD=90°,
∴∠ACB=90°﹣∠DBC
∠ABD=90°﹣∠A,
∵∠A=2∠DBC,
∴∠ABD=90°﹣2∠DBC
∴∠ABC=∠ABD+∠DBC
=90°﹣2∠DBC+∠DBC
=90°﹣∠DBC,
∴∠ACB=∠ABC,
(3)∵∠ABC=∠F+∠BCF
∠ABC=∠ABE+∠EBC
∠BCF=2∠ABE
∴∠EBC=∠F+∠ABE,
∵∠ABC=∠ACB,
∴∠ACB=2∠ABE+∠F,
∵∠F=∠BEC
∠EBC+∠ECB+∠BEC=180°,
∴∠F+∠ABE+2∠ABE+∠F+∠F=180°,
∴3∠F+3∠ABE=180°,
∴∠F+∠ABE=60°,
∴∠EBC=60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且 ;将
;将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 ,连结
,连结 、
、 ,下列结论中,正确的个数为( )
,下列结论中,正确的个数为( )①
 ;②
;② ;③
;③ ;④
;④

A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )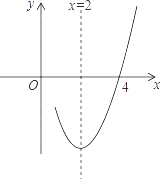
A.①②③
B.③④⑤
C.①②④
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=﹣1(a<b)的两根,则实数x1 , x2 , a,b的大小关系是( )
A.a<x1<x2<b
B.x1<a<x2<b
C.x1<a<b<x2
D.x1<x2<a<b -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
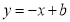 经过点
经过点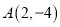 ,且与
,且与 交于点
交于点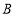 ,在
,在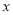 轴上存在一点
轴上存在一点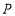 使得
使得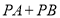 的值最小,则点
的值最小,则点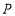 的坐标为_______.
的坐标为_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会向全校
 名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:(1)本次接受随机抽样调查的学生人数为 人,图
 中
中 的值是 .
的值是 .(2)补全图2的统计图.
(3)求本次调查获取的样本数据的平均数、众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为
 元的学生人数.
元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数y=ax2+(a2﹣1)x﹣a的图象与x轴的一个交点的坐标为(m,0).若2<m<3,则a的取值范围是 .
相关试题

