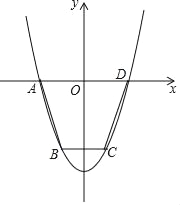
【题目】如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标.
参考答案:
【答案】(1)y=x2﹣4;(2)M(0,﹣2)
【解析】(1)将A、B点的坐标代入抛物线的解析式中即可求出待定系数的值;
(2)由于A、D关于抛物线对称轴即y轴对称,那么连接BD,BD与y轴的交点即为所求的M点,可先求出直线BD的解析式,即可得到M点的坐标;
解:(1)由题意可得:![]() ,
,
解得![]() ;
;
∴抛物线的解析式为:y=x2﹣4;
(2)由于A、D关于抛物线的对称轴(即y轴)对称,连接BD.
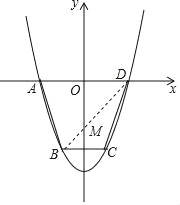
则BD与y轴的交点即为M点;
设直线BD的解析式为:y=kx+b(k≠0),则有:
![]() ,
,
解得![]() ;
;
∴直线BD的解析式为y=x﹣2,
∴点M(0,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE =12,CE =5,则平行四边形ABCD的周长是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是一个边长为 6 的正方形,点
是一个边长为 6 的正方形,点  在
在  的延长线上,连接
的延长线上,连接  ,过
,过 作
作  的垂线,交
的垂线,交  的延长线于点
的延长线于点  ,且
,且  ,则
,则  _____.
_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,高
,高 、
、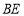 相交于点
相交于点 ,
,  ,且
,且 .
.(1)求线段
 的长;
的长;(2)动点
 从点
从点  出发,沿线段
出发,沿线段  以每秒 1 个单位长度的速度向终点
以每秒 1 个单位长度的速度向终点  运动,动点
运动,动点  从 点
从 点  出发沿射线
出发沿射线 以每秒 4 个单位长度的速度运动,
以每秒 4 个单位长度的速度运动, 两点同时出发,当点
两点同时出发,当点  到达
到达  点时,
点时, 两点同时停止运动.设点
两点同时停止运动.设点  的运动时间为
的运动时间为  秒,
秒, 的面积为
的面积为  ,请用含
,请用含 的式子表示
的式子表示  ,并直接写出相应的
,并直接写出相应的  的取值范围;
的取值范围;(3)在(2)的条件下,点
 是直线
是直线 上的一点且
上的一点且  .是否存在
.是否存在 值,使以点
值,使以点  为顶 点的三角形与以点
为顶 点的三角形与以点  为顶点的三角形全等?若存在,请直接写出符合条件的
为顶点的三角形全等?若存在,请直接写出符合条件的  值; 若不存在,请说明理由.
值; 若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF

(1)求证:△ABE≌△ADF
(2)过点C作CG‖EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC
的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


相关试题

