【题目】如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数.

参考答案:
【答案】100°
【解析】试题设∠BAD=x.由AD平分∠BAC,得出∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.由AC=BC,得出∠B=∠BAC=2x.根据三角形外角的性质得出∠ADC=∠B+∠BAD=60°,即2x+x=60°,求得x=20°,那么∠B=∠BAC=40°.然后在△ABC中,根据三角形内角和定理得出∠C=180°-∠B-∠BAC=100°.
试题解析:设∠BAD=x.
∵AD平分∠BAC,
∴∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.
∵AC=BC,
∴∠B=∠BAC=2x.
∵∠ADC=∠B+∠BAD=60°,
∴2x+x=60°,
∴x=20°,
∴∠B=∠BAC=40°.
在△ABC中,∵∠BAC+∠B+∠C=180°,
∴∠C=180°-∠B-∠BAC=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
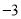
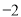

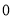
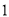
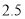
筐 数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价
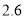 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(直接写出结果):
(1)﹣2+5
(2)﹣17+(﹣3)
(3)(﹣10)﹣(-6)
(4)(﹣1
 )×(﹣12)
)×(﹣12) (5)﹣2×(﹣3)2
(6)﹣1
 ÷(﹣5)
÷(﹣5) (7)﹣1200+(﹣1)200
(8)﹣0.125×(﹣2)3
(9)|﹣
 |
| (10)(-
 )3
)3 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-5.5)+(-3.2)-(-2.5)-4.8
(2)-40-28-(-19)+(-24)
(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=30 cm,BC=35 cm,∠B=60°,有一动点M自A向B以1 cm/s的速度运动,动点N自B向C以2 cm/s的速度运动,若M,N同时分别从A,B出发.
(1)经过多少秒,△BMN为等边三角形;
(2)经过多少秒,△BMN为直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

相关试题

