23. --- I try to memorize new words every day, but can only remember few of them.

　　 --- That’s not surprising. Newly – learnt words are easily forgotten unless frequently 　　　

in communication.

　　　 A. used　　　　　　　　　 B. using　　　　　　　　　 C. to use　　　　　　　　 D. be used

22. It took the early settlers more than 150 years to build up 　　　　is now a modem city.

　　　 A. where　　　　　　　　 B. which　　　　　　　　 C. what　　　　　　　　　 D. that

第一节：单项填空(共15小题，每小题1分，满分15分)

从A、B、C、D四个选项中，选出可以填入空白处的最佳选项。

21. --- Let’s discuss the question raised last night, shall we?

　　 --- There is no hurry for that. I 　　　　for a conference.

　　　 A. headed　　　　　　 B. was heading　　 C. am heading　　 D. have headed

2．　 在某次交通事故中，交警测量汽车刹车线的长，用以判断该车是否超速。请问还需什么数据，如何计算？(还应知汽车最大制动加速度)

在解答本题前可让学生分析一下发生交通事故的可能原因；略

问：汽车在反应距离做什么运动？(匀速)汽车在刹车距离做什么运动？(匀减速)反应距离跟哪些有关系？(反应时间及刹车时的速度)刹车距离跟哪些有关系？(刹车时的速度及刹车的加速度)

4.5m那么这辆轿车的加速度约为(　　 )

A　 1m/s；　 B　 2m/s；　 C　 3m/s；　 D　 4m/s；　 (答：B)

2．(1999年上海高考题)为了测定某轿车在平直路上运动时的加速度(轿车启动时的运动可以近似看做匀加速运动)，某人拍摄了一张在同一底片上多次曝光的照片(如图)，如果拍摄时每隔2s曝光一次，轿车车身总长为

1．　 某航空母舰上飞机在跑道加速时，发动机最大加速度为5m/s²，所需起飞速度为50m/s，跑道长100m，通过计算判断，飞机能否靠自身发动机从舰上起飞？为了使飞机在开始滑行时就有一定的初速度，航空母舰装有弹射装置，对于该型号的舰载飞机，弹射系统必须使它具有多大的初速度？(答：不能靠自身发动机起飞；39m/s。)

初中已学过匀速直线运动求位移的方法x=vt,在速度-时间图像中可看出位移对应着一块矩形面积。(此处让学生思考回答)

　对于匀变速直线运动是否也对应类似关系呢？

☺ 引入新课

分析书上 “思考与讨论” ，引入微积分思想，对书P41图2.3-2的分析理解(教师与学生互动)确认v-t图像中的面积可表示物体的位移。

☺ 位移公式推导：

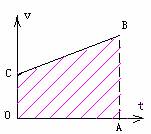先让学生写出梯形面积表达式：

S=(OC+AB)OA/2

分请学生析OC,AB,OA各对应什么物理量？并将v = v₀ + at 代入，

得出：x = v₀t + at²/2

注意式中x, v₀ ,a要选取统一的正方向。

☺ 应用：1。书上例题分析，按规范格式书写。

2．补充例题：汽车以10s的速度行驶，刹车加速度为5m/s，求刹车后1s，2s，3s的位移。

　　　　 已知： v= 10m/s,　 a= -5m/s²。

由公式：x = v₀t + at²/2

可解出：x₁ = 10*1 - 5*1²/2 = 7.5m

　　　　　 x₂ = 10*2 - 5*2²/2 = 10m

　　　　　 x₃ = 10*3 - 5*3²/2 = 7.5m ？

由x₃=7.5m学生发现问题：汽车怎么往回走了？

结合该问题教师讲解物理知识与实际问题要符合，实际汽车经2S已

经停止运动，不会往回运动，所以3S的位移应为10米。事实上汽车在大于2S的任意时间内位移均为10m。

☺ 匀变速直线运动的位移与速度的关系：

　　 如果我们所研究的问题不涉及时间，而仍用v=v₀+at 和x=v₀t+at²/2会显得繁琐。在以上两公式中消去时间t，所得的结果直接用于解题，可使不涉及时间的问题简洁起来。

　　　 由：v = v₀ + at

　　　　　 x = v₀t + at²/2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　 消去t，得v² - v₀² = 2ax　 (注意：该式为不独立的导出式)

　　　 ☺ 练习：由前面例题：v₀ =10m/s,　 a = -5m/s² 求刹车经7.5m时的速度？

　　　　　　 由公式：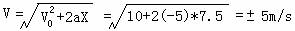

　　　　　　　　　　 v = -5m/s　 (舍去)

　　　　 　　刹车经7.5米时的速度为5m/s,与初速度方向相同。

☺ 补充练习：

2．　 速度-时间图象中面积表示位移。

1．　 公式中各物理量的理解与准确应用。