初中已学过匀速直线运动求位移的方法x=vt,在速度-时间图像中可看出位移对应着一块矩形面积。(此处让学生思考回答)

　对于匀变速直线运动是否也对应类似关系呢？

☺ 引入新课

分析书上 “思考与讨论” ，引入微积分思想，对书P41图2.3-2的分析理解(教师与学生互动)确认v-t图像中的面积可表示物体的位移。

☺ 位移公式推导：

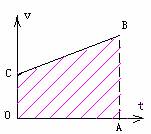先让学生写出梯形面积表达式：

S=(OC+AB)OA/2

分请学生析OC,AB,OA各对应什么物理量？并将v = v₀ + at 代入，

得出：x = v₀t + at²/2

注意式中x, v₀ ,a要选取统一的正方向。

☺ 应用：1。书上例题分析，按规范格式书写。

2．补充例题：汽车以10s的速度行驶，刹车加速度为5m/s，求刹车后1s，2s，3s的位移。

　　　　 已知： v= 10m/s,　 a= -5m/s²。

由公式：x = v₀t + at²/2

可解出：x₁ = 10*1 - 5*1²/2 = 7.5m

　　　　　 x₂ = 10*2 - 5*2²/2 = 10m

　　　　　 x₃ = 10*3 - 5*3²/2 = 7.5m ？

由x₃=7.5m学生发现问题：汽车怎么往回走了？

结合该问题教师讲解物理知识与实际问题要符合，实际汽车经2S已

经停止运动，不会往回运动，所以3S的位移应为10米。事实上汽车在大于2S的任意时间内位移均为10m。

☺ 匀变速直线运动的位移与速度的关系：

　　 如果我们所研究的问题不涉及时间，而仍用v=v₀+at 和x=v₀t+at²/2会显得繁琐。在以上两公式中消去时间t，所得的结果直接用于解题，可使不涉及时间的问题简洁起来。

　　　 由：v = v₀ + at

　　　　　 x = v₀t + at²/2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　 消去t，得v² - v₀² = 2ax　 (注意：该式为不独立的导出式)

　　　 ☺ 练习：由前面例题：v₀ =10m/s,　 a = -5m/s² 求刹车经7.5m时的速度？

　　　　　　 由公式：

　　　　　　　　　　 v = -5m/s　 (舍去)

　　　　 　　刹车经7.5米时的速度为5m/s,与初速度方向相同。

☺ 补充练习：