科目：已知命题p：若x＝y，则x2＝y2，那么命题非p是A.若x＝y，则x2≠y2B.若x≠y，则x2≠y2C.若x≠y，则x2＝y2D.若x2＝y2，则x＝y，来源：，题型：单选题

已知命题p：若x＝y，则x2＝y2，那么命题非p是


  1. A.
    若x＝y，则x2≠y2
  2. B.
    若x≠y，则x2≠y2
  3. C.
    若x≠y，则x2＝y2
  4. D.
    若x2＝y2，则x＝y
点击展开完整题目
查看答案和解析>>
科目：3不小于2的否定形式是A.3≥2B.3＞2C.3＜2D.3≤2，来源：，题型：单选题

3不小于2的否定形式是


  1. A.
    3≥2
  2. B.
    3＞2
  3. C.
    3＜2
  4. D.
    3≤2
点击展开完整题目
查看答案和解析>>
科目：下列语句是复合命题的是两点确定一条直线-3不大于0任何集合都不是空集的子集x＝±2是方程x2＝4的根A.B.C.D.，来源：，题型：单选题

下列语句是复合命题的是
①两点确定一条直线
②-3不大于0
③任何集合都不是空集的子集
④x＝±2是方程x2＝4的根


  1. A.
    ①②
  2. B.
    ③④
  3. C.
    ②③④
  4. D.
    ①③④
点击展开完整题目
查看答案和解析>>
科目：下列命题是简单命题的是A.菱形的对角线垂直平分B.3＜5C.24是3和4的倍数D.2≥0，来源：，题型：单选题

下列命题是简单命题的是


  1. A.
    菱形的对角线垂直平分
  2. B.
    3＜5
  3. C.
    24是3和4的倍数
  4. D.
    2≥0
点击展开完整题目
查看答案和解析>>
科目：函数f(x)定义在R上，常数a≠0，下列正确的命题个数是若f(a+x)＝f(a-x)，则函数y＝f(x)的对称轴是直线x＝a函数y＝f(a+x)和y＝f(a-x)的对称轴是x＝0若f(a-x)＝f(x-a)，则函数y＝f(x)的对称轴是x＝0函数y＝f(x-a)和y＝f(a-x)的图象关于直线x＝a对称A.1B.2C.3D.4，来源：，题型：单选题

函数f(x)定义在R上，常数a≠0，下列正确的命题个数是
①若f(a+x)＝f(a-x)，则函数y＝f(x)的对称轴是直线x＝a
②函数y＝f(a+x)和y＝f(a-x)的对称轴是x＝0
③若f(a-x)＝f(x-a)，则函数y＝f(x)的对称轴是x＝0
④函数y＝f(x-a)和y＝f(a-x)的图象关于直线x＝a对称


  1. A.
    1
  2. B.
    2
  3. C.
    3
  4. D.
    4
点击展开完整题目
查看答案和解析>>
科目：一个凸多边形的内角成等差数列，其中最小的内角为120°，公差为5°，那么这个多边形的边数n等于A.12B.16C.9D.16或9，来源：，题型：单选题

一个凸多边形的内角成等差数列，其中最小的内角为120°，公差为5°，那么这个多边形的边数n等于


  1. A.
    12
  2. B.
    16
  3. C.
    9
  4. D.
    16或9
点击展开完整题目
查看答案和解析>>
科目：给定正数p，q，a，b，c，其中p≠q，若p，a，q是等比数列，p，b，c，q是等差数列，则一元二次方程bx2-2ax+c=0A.无实根B.有两个相等实根C.有两个同号相异实根D.有两个异号实根，来源：，题型：单选题

给定正数p，q，a，b，c，其中p≠q，若p，a，q是等比数列，p，b，c，q是等差数列，则一元二次方程bx2-2ax+c=0


  1. A.
    无实根
  2. B.
    有两个相等实根
  3. C.
    有两个同号相异实根
  4. D.
    有两个异号实根
点击展开完整题目
查看答案和解析>>
科目：设有如下三个命题：甲：相交直线l、m都在平面α内，并且都不在平面β内；乙：直线l、m中至少有一条与平面β相交；丙：平面α与平面β相交．当甲成立时A.乙是丙的充分而不必要条件B.乙是丙的必要而不充分条件C.乙是丙的充分且必要条件D.乙既不是丙的充分条件又不是丙的必要条件，来源：，题型：单选题

设有如下三个命题：
甲：相交直线l、m都在平面α内，并且都不在平面β内；
乙：直线l、m中至少有一条与平面β相交；
丙：平面α与平面β相交．
当甲成立时


  1. A.
    乙是丙的充分而不必要条件
  2. B.
    乙是丙的必要而不充分条件
  3. C.
    乙是丙的充分且必要条件
  4. D.
    乙既不是丙的充分条件又不是丙的必要条件
点击展开完整题目
查看答案和解析>>
科目：设球的体积为V1，它的内接正方体的体积为V2，下列说法中最合适的是A.V1比V2大约多一半B.V1比V2大约多两倍半C.V1比V2大约多一倍D.V1比V2大约多一杯半，来源：，题型：单选题

设球的体积为V1，它的内接正方体的体积为V2，下列说法中最合适的是


  1. A.
    V1比V2大约多一半
  2. B.
    V1比V2大约多两倍半
  3. C.
    V1比V2大约多一倍
  4. D.
    V1比V2大约多一杯半
点击展开完整题目
查看答案和解析>>
科目：有一个容量为200的样本，其频率分布直方图如图所示，根据样本的频率分布直方图估计，样本数据落在区间[10，12)内的频数为A.18B.36C.54D.72，来源：，题型：单选题

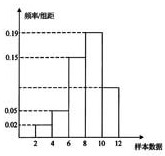有一个容量为200的样本，其频率分布直方图如图所示，根据样本的频率分布直方图估计，样本数据落在区间[10，12）内的频数为


  1. A.
    18
  2. B.
    36
  3. C.
    54
  4. D.
    72
点击展开完整题目
查看答案和解析>>
关闭