【题目】已知圆心在 ![]() 轴上的圆
轴上的圆 ![]() 过点
过点 ![]() 和
和 ![]() ,圆
,圆 ![]() 的方程为
的方程为 ![]() .
.
(1)求圆 ![]() 的方程;
的方程;
(2)由圆 ![]() 上的动点
上的动点 ![]() 向圆
向圆 ![]() 作两条切线分别交
作两条切线分别交 ![]() 轴于
轴于 ![]() ,
, ![]() 两点,求
两点,求 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】
(1)设 , ,
依题意得,圆 的圆心为线段 的垂直平分线 ![]() 与 轴的交点 .
与 轴的交点 .
因为直线 ![]() 的方程为 ,即 ,
的方程为 ,即 ,
所以圆心 的坐标为 .
所以圆 的方程为 .
(2)设圆 上的动点 的坐标为 ,
则 ,
即 ,
解得 .
设点 , ,
则直线 : ,即 ,
因为直线 与圆 相切,所以 ,
化简得 . ①
同理得 , ②
由①②知 , 为方程 的两根,
即 
所以
.
因为 ,
所以
.
令 ,因为 ,所以 .
所以 ,
当 时, ![]() ,
,
当 时, .
所以 的取值范围为 .
【解析】分析:本题主要考查了圆方程的综合应用,解决问题的关键是(1)先设圆的标准方程,再利用已知条件可得 ![]() 和
和 ![]() 的值,即可得圆
的值,即可得圆 ![]() 的方程;(2)先设圆
的方程;(2)先设圆 ![]() 上的动点
上的动点 ![]() 的坐标为
的坐标为 ![]() ,则可得
,则可得 ![]() 的取值范围,再写出
的取值范围,再写出 ![]() ,
, ![]() 的方程,可得
的方程,可得 ![]() 和
和 ![]() 的坐标,进而可得
的坐标,进而可得 ![]() ,利用函数的单调性,可得
,利用函数的单调性,可得 ![]() 的最大值和最小值,即可得
的最大值和最小值,即可得 ![]() 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在
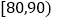 的人数为12人.
的人数为12人.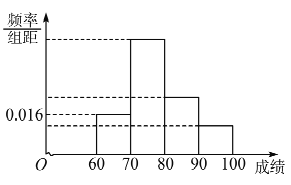
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为
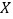 ,求
,求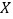 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足 ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an},满足d>0,且a1+a2+a3=9,a1a3=5
(1)求{an}的通项公式;
(2)若数列{bn}满足bn=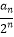 ,Sn为数列{bn}的前n项和,证明:Sn<3.
,Sn为数列{bn}的前n项和,证明:Sn<3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+
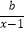 (ab≠0).
(ab≠0).
(1)当b=a=1时,求函数f(x)的单调区间;
(2)若函数f(x)在点(2,f(2))处的切线方程是y=2x﹣3,证明:曲线y=f(x)上任一点处的切线与直线x=1和直线y=x所围成的三角形面积为定值,并求出此定值. -
科目: 来源: 题型:
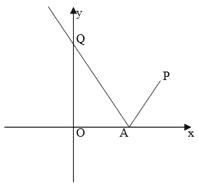
查看答案和解析>>【题目】如图,已知过点
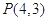 的光线,经
的光线,经 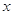 轴上一点
轴上一点 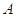 反射后的射线
反射后的射线  过点
过点 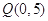 .
. 
(1)求点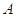 的坐标;
的坐标;
(2)若圆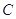 过点
过点 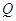 且与
且与 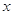 轴相切于点
轴相切于点 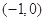 ,求圆
,求圆 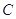 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明:对一切x∈(0,+∞),都有lnx> ﹣
﹣  成立.
成立.
相关试题

