【题目】如图,已知过点 ![]() 的光线,经
的光线,经 ![]() 轴上一点
轴上一点 ![]() 反射后的射线
反射后的射线 ![]() 过点
过点 ![]() .
. 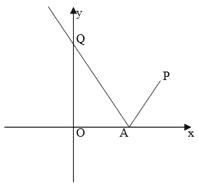
(1)求点 ![]() 的坐标;
的坐标;
(2)若圆 ![]() 过点
过点 ![]() 且与
且与 ![]() 轴相切于点
轴相切于点 ![]() ,求圆
,求圆 ![]() 的方程.
的方程.
参考答案:
【答案】
(1)由光线的反射角与入射角相等可知,
点 关于 轴对称点 在射线 ![]() ,
,
射线 ![]() 所在的直线方程为
所在的直线方程为 ![]() ,
,
即 ,令 ,则 ,
点 的坐标为 .
(2)设圆 的方程为 ,
圆 与 轴相切于点 ,
,
圆 过点 ,
,
解得 ,
圆 的方程为 .
【解析】分析:本题主要考查了直线和圆的方程的应用,解决问题的关键是(1)点 ![]() 关于
关于 ![]() 轴对称点
轴对称点 ![]() 在射线
在射线 ![]() ,所以先求入射光线所在直线的方程,然后再求与
,所以先求入射光线所在直线的方程,然后再求与 ![]() 轴的交点;(2)首先设圆的标准方程为
轴的交点;(2)首先设圆的标准方程为 ![]() ,然后与
,然后与 ![]() 轴相切于点
轴相切于点 ![]() 得到圆心的纵坐标与半径相等,圆心的横坐标等于-1,又过点
得到圆心的纵坐标与半径相等,圆心的横坐标等于-1,又过点 ![]() ,代入求得圆的方程.
,代入求得圆的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an},满足d>0,且a1+a2+a3=9,a1a3=5
(1)求{an}的通项公式;
(2)若数列{bn}满足bn=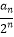 ,Sn为数列{bn}的前n项和,证明:Sn<3.
,Sn为数列{bn}的前n项和,证明:Sn<3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在
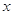 轴上的圆
轴上的圆 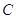 过点
过点 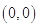 和
和 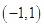 ,圆
,圆 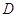 的方程为
的方程为 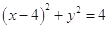 .
.
(1)求圆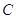 的方程;
的方程;
(2)由圆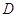 上的动点
上的动点 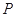 向圆
向圆 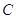 作两条切线分别交
作两条切线分别交 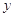 轴于
轴于 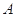 ,
, 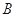 两点,求
两点,求 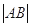 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+
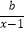 (ab≠0).
(ab≠0).
(1)当b=a=1时,求函数f(x)的单调区间;
(2)若函数f(x)在点(2,f(2))处的切线方程是y=2x﹣3,证明:曲线y=f(x)上任一点处的切线与直线x=1和直线y=x所围成的三角形面积为定值,并求出此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明:对一切x∈(0,+∞),都有lnx> ﹣
﹣  成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的定义域,判断并证明
的定义域,判断并证明 的奇偶性;
的奇偶性;(2)判断函数
 的单调性;
的单调性;(3)解不等式
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
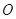 的圆心为原点
的圆心为原点 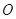 ,且与直线
,且与直线 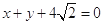 相切。
相切。 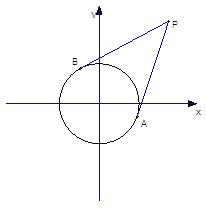
(1)求圆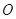 的方程;
的方程;
(2)过点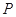 (8,6)引圆O的两条切线
(8,6)引圆O的两条切线 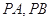 ,切点为
,切点为 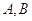 ,求直线
,求直线 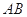 的方程.
的方程.
相关试题

