【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ![]() ,求使得不等式
,求使得不等式 ![]() 恒成立的实数k的取值范围.
恒成立的实数k的取值范围.
参考答案:
【答案】
(1)解:由3Sn=4an﹣4可得a1=4,
∵3Sn=4an﹣4,∴3Sn﹣1=4an﹣1﹣4,∴3Sn﹣3Sn﹣1=4an﹣4﹣(4an﹣1﹣4),
∴3an=4an﹣4an﹣1,即 ![]() .
.
∴数列{an}是首项为a1=4,公比为4的等比数列,∴ ![]() .
.
又bn=log2a1+log2a2+…+log2an=2+4+…+2(n﹣1)+2n=n(n+1),
∴bn=n(n+1)
(2)解: ![]() =1﹣
=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
不等式 ![]() 恒成立,即k≥
恒成立,即k≥ ![]() 恒成立,
恒成立,
设dn= ![]() ,则dn+1﹣dn=
,则dn+1﹣dn= ![]() ,
,
∴当n≥2时,数列{dn}单调递减,当1≤n<2时,数列{dn}单调递增;
即d1<d2>d3>d4>…,
∴数列最大项为 ![]() ,∴
,∴ ![]()
【解析】(1)利用再写一式,两式相减的方法求数列{an}的通项公式、利用数列{bn}满足bn=log2a1+log2a2+…+log2an , 求出{bn}的通项公式;(2)若 ![]() ,裂项求和,不等式
,裂项求和,不等式 ![]() 恒成立,即k≥
恒成立,即k≥ ![]() 恒成立,即可实数k的取值范围.
恒成立,即可实数k的取值范围.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系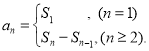 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2+2x+b>0(a≠0)的解集为
 ,且a>b,则
,且a>b,则  的最小值是 .
的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
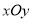 中,直线
中,直线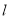 的参数方程为
的参数方程为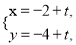 (
(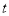 为参数).以原点
为参数).以原点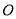 为极点,
为极点, 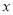 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线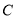 的极坐标方程为
的极坐标方程为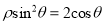 .直线
.直线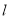 交曲线
交曲线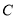 于
于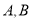 两点.
两点.(1)写出直线
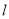 的极坐标方程和曲线
的极坐标方程和曲线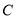 的直角坐标方程;
的直角坐标方程;(2)设点
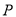 的直角坐标为
的直角坐标为 ,求点
,求点 到
到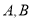 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
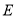 的顶点为原点
的顶点为原点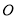 ,焦点为圆
,焦点为圆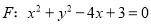 的圆心
的圆心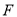 .经过点
.经过点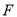 的直线
的直线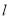 交抛物线
交抛物线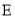 于
于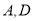 两点,交圆
两点,交圆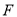 于
于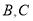 两点,
两点, 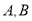 在第一象限,
在第一象限, 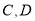 在第四象限.
在第四象限.(1)求抛物线
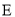 的方程;
的方程;(2)是否存在直线
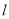 ,使
,使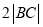 是
是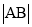 与
与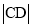 的等差中项?若存在,求直线
的等差中项?若存在,求直线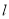 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是自然对数的底数,
是自然对数的底数,  ,
,  ,
,  ,
,  .
.(1)设
 ,求
,求 的极值;
的极值;(2)设
 ,求证:函数
,求证:函数 没有零点;
没有零点;(3)若
 ,设
,设 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在四棱柱
 中,点
中,点 分别为
分别为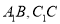 的中点.
的中点.
(1)求证:
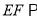 平面
平面 ;
;(2)若四棱柱
 是长方体,且
是长方体,且 ,求平面
,求平面 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 且
且 ),
), 为自然对数的底数.
为自然对数的底数.(Ⅰ)当
 时,求函数
时,求函数 在区间
在区间 上的最大值;
上的最大值;(Ⅱ)若函数
 只有一个零点,求
只有一个零点,求 的值.
的值.
相关试题

